Física Electromagnetismo Campo Magnético
Tabla de contenidos
Campo Magnético
El campo magnético es la descripción de cómo interactúan imanes, corrientes y cargas eléctricas en movimiento. Al igual que el campo eléctrico o el gravitatorio, es un campo vectorial, por lo que cada punto del espacio está dotado de una magnitud, dirección y sentido. Se mide en Teslas
T = kg/(A s^2) = V s/m^2
Podemos describirlo a partir de la ley de Gauss para el magnetismo, la ley de Ampère-Maxwell y la de Biot-Savart:
Forma diferencial
\nabla \cdot \vec{B} = 0
\nabla \times \vec{B} = \mu_0 \vec{J} + \mu_0 \epsilon_0 \frac{\partial \vec{E}}{\partial t}
d\vec{B} = \frac{\mu_0}{4\pi}\frac{I d\vec{l}\times \hat{r}}{r^2}
Forma integral
\int_S \vec{B} \cdot d\vec{S} = 0
\int_{\partial S} \vec{B}\cdot d\vec{l} = \mu_0 I + \mu_0 \epsilon_0 \frac{\partial \Phi _E}{\partial t}
\vec{B} = \frac{\mu_0}{4\pi}\int_{C}\frac{I d\vec{l} \times (\vec{r} – \vec{r}')}{|\vec{r}-\vec{r}'|^{3}}
Nombre
Ley de Gauss para el magnetismo
Ley de Ampère-Maxwell
Ley de Biot-Savart
Vamos a explicar estas tres fórmulas.
La primera, la ley de Gauss para el magnetismo, es análoga a la ley de Gauss eléctrica y gravitatoria y nos dice que las líneas de campo magnético son cerradas, es decir, nacen y mueren en el mismo punto; toda superficie que rodee un imán será atravesada por tantas líneas entrantes como salientes:

En esta imagen donde se ha situado un imán sobre pequeños filamentos de metal se pueden ver las líneas de campo como éstas salen de un lado y entran por el otro (no podemos saber cual es cual) y como éstas son todas cerradas.
Esta ley implica también la no existencia de los monopolos magnéticos, sin embargo, esto no está demostrado y se están buscando, pero todavía no se ha visto ninguno; todos los imanes tienen por lo menos un polo negativo y uno positivo.
La segunda ley, la de Ampère-Maxwell nos habla de las fuentes que crean este campo magnético, las cuales son las corrientes eléctricas I y los cambios temporales en el flujo de campo eléctrico \frac{\partial \Phi_{E}}{\partial t}. La ley se lee como: la integral sobre la frontera de una superficie (por ejemplo el perímetro de un cuadrado) es proporcional a la intensidad que atraviesa la superficie y el cambio temporal del campo eléctrico en su interior. Las constantes de proporción que las relaciona son la permeabilidad magnética del vacío \mu_0 = 4\pi \, 10^{-7} H/m \, o \, T m /A la permitividad dieléctrica del vacío \epsilon_0 = 8.85 \cdot 10^{-12}. Esta ley es útil para sistemas con alta simetría como hilos conductores infinitos o solenoides infinitos.
La tercera nos permite calcular al campo en un punto \vec{r} dada sumando cada contribución d\vec{l} de una distribución de intensidad C, esta fórmula sirve para cualquier caso, a veces es más fácil usar ésta y a veces la ley de Ampère-Maxwell.
Pongamos 3 ejemplos: un hilo infinito recto por el que circula una corriente constante I, una espira (un hilo circular) y un solenoide (una bobina o muelle) por el que circulan la misma corriente:
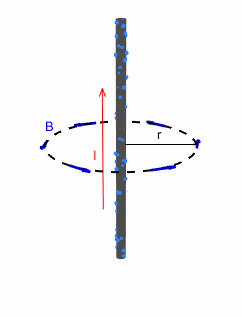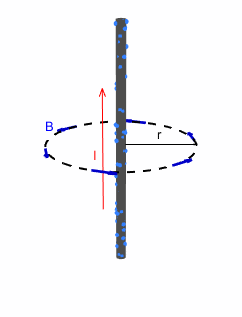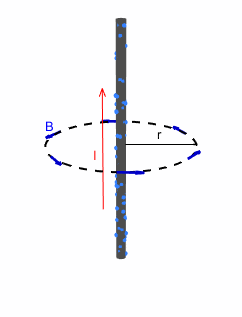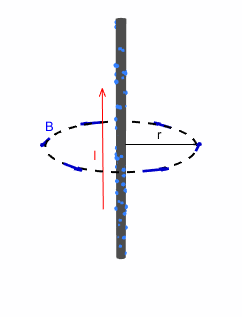
.Empecemos por el hilo infinito:
Campo creado por un hilo infinito
Si tomamos un vector d\vec{l} que siga un pequeño elemento de la circunferencia, podemos ver que \vec{B} es tangente a d\vec{l} en todo punto, así que \vec{B}\cdot d\vec{l} = B \, dl , además, \vec{B} es constante en módulo a lo largo de toda la espira y sigue la dirección y sentido del vector angular \hat{\theta} = (- sin(\theta), cos(\theta), 0) en coordenadas cilíndricas. El campo eléctrico es constante, puesto que la corriente lo es, así que \frac{\partial \Phi _{E}}{\partial t} = 0. Como la longitud de la circunferencia es l = 2\pi r y la corriente que atraviesa el circulo es I, entonces:
\int_{\partial S}\vec{B}\cdot d\vec{l} = \int_{\partial S} B \, dl = B \int_{\partial S} dl = B \, 2\pi r = \mu_0 I \rightarrow B = \frac{\mu_0 I}{2 \pi r} \rightarrow \vec{B} = \frac{\mu_0 I}{2 \pi r}\, \hat{\theta}
Ahora calculemos el segundo caso:
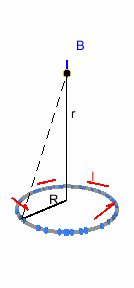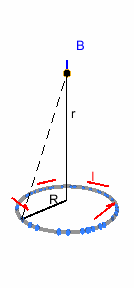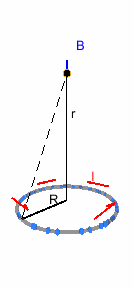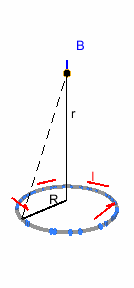
Campo creado por una espira en su eje
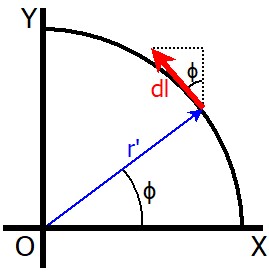
Queremos calcular el campo inducido en una posición \bf{\vec{r} = (0, 0, r)}. \bf{\vec{r}'} une el origen con la espira, así que \bf{\vec{r}' = (R \, cos(\phi), R \, sin(\phi),0)}, con \phi el ángulo azimutal (contenido en el plano de la espira). d\vec{l} es un vector que sigue tangencialmente a la espira, así que es \bf{d\vec{l} = R\,(-sin(\phi), cos(\phi),0)d\theta}.
La diferencia de los vectores es: \bf{\vec{r}-\vec{r}' = ( – \, Rcos(\phi),-Rsin(\phi),r)}
Con esto ya podemos calcular la integral
El producto vectorial de d\vec{l} \times (\vec{r}-\vec{r}') \, = \, \left| \begin{matrix} \hat{x} & \hat{y} & \hat{z} \\ -R\, sin(\phi) & R \, cos(\phi) & 0 \\ – R \, cos(\phi) & -R \, sin(\phi) & r \end{matrix} \right| = (r\,R\, cos \phi, r \, R \, sin \phi, R^2)
Y el módulo de la diferencia, |\vec{r} – \vec{r}'| = \sqrt{( R \, cos \phi)^2 + (R \, sin \phi )^2 + r^2} = \sqrt{r^2 + R^2}
\vec{B} = \frac{\mu_0 \, I}{4\pi}\int_{0}^{2\pi}d\phi \frac{(r\,R\, cos \phi, r \, R \, sin \phi, R^2) }{(r^2 + R^2)^{3/2}}
B_y = \frac{\mu_0 I \, r\,R}{4\pi (r^2 + R^2)^{3/2}}\int_{0}^{2\pi} sin \phi \, d\phi
B_x = \frac{\mu_0 I \, R^2}{4\pi (r^2 + R^2)^{3/2}}\int_{0}^{2\pi} \, d\phi
En las 2 primeras estamos integrando sin \phi y cos \phi en un periodo entero \rightarrow la integral da 0.
La tercera componente de la integral es inmediata, resultando que
\vec{B} = (0,0,\frac{\mu_0 \, I \, R^2}{2 (r^2 + R^2)^{3/2}})
Campo creado por una bobina en su eje
Para este caso vamos a emplear de vuelta la ley de Ampère-Maxwell. Siendo que el campo eléctrico es constante, el segundo término \frac{\partial \Phi_E}{\partial t}=0.
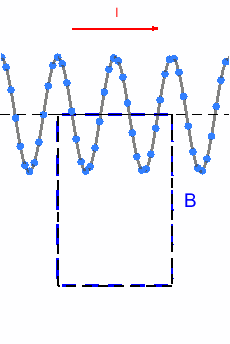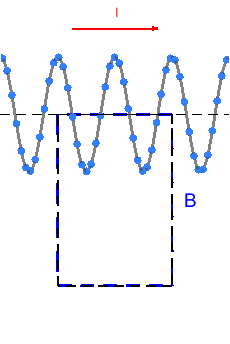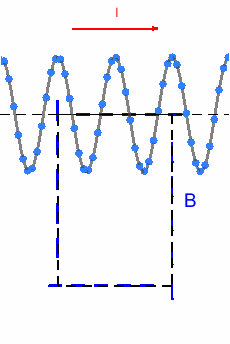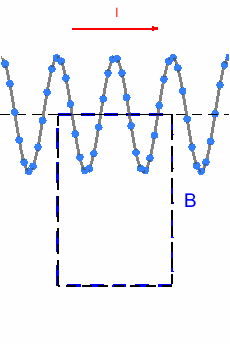
En este ejemplo, la línea que vamos a emplear es un rectángulo. Primero queremos calcular la corriente que encierra el rectángulo. Si el lado superior tiene una longitud L y la bobina tiene n vueltas por metro, entonces la intensidad que la circula será I_{enc} = n \,L \,I.
Ahora vamos con la integral. Como estamos integrando sobre una línea, podemos dividir la integral en 4, una por cada lado del rectángulo:
\int_{rectángulo} \vec{B}\cdot d\vec{l} = \int_{arriba}\vec{B}\cdot d\vec{l} + \int_{abajo}\vec{B}\cdot d\vec{l} + \int_{izquierda}\vec{B}\cdot d\vec{l} + \int_{derecha}\vec{B}\cdot d\vec{l}
Podemos calcularlos de la siguiente manera
- Si hacemos el rectángulo muy alargado, situando el lado inferior muy lejos, el campo en ese punto será muy pequeño y podemos despreciar ese término.
- Fijándonos en la animación, podemos ver que el lado izquierdo y derecho tienen igual longitud (es un rectángulo) y cada punto donde el campo sube por el izquierdo hay uno igual donde baja por el derecho, entonces \int_{izquierda} \vec{B}\cdot d\vec{l} + \int_{derecha}\vec{B}\cdot d\vec{l} = 0.
- Sólo nos queda el tramo de arriba. Como d\vec{l} va a la derecha y \vec{B}, también, \vec{B}\cdot d\vec{l} = B\,dl , además, el campo es constante a lo largo de toda la línea, así que, \int_{arriba}\vec{B}\cdot d\vec{l} = B \int_{arriba}dl = B \, L.
Juntando todo esto tenemos que:
B \, L = \mu_0 \, n \, L \, I \rightarrow B = \mu_0 \, n \, I
\vec{B} va hacia la derecha y en dirección del eje del solenoide. Es importante notar que el campo en el interior es constante, no hemos fijado que se encuentre justo en el eje de la bobina, además, el campo en el exterior es nulo, es decir, los solenoides son creadores de campo magnético muy aislados, no interfieren con el exterior y en el interior es constante.
Comparación de fuentes de campo
Una vez hemos calculado las fuentes más comunes de campo magnético, vamos a compararlas entre ellas:
La intensidad va a ser igual para las 3 y es de 0.1 A. Calcularemos el campo del hilo a una distancia R = 5cm, que es, además el radio de la espira y del solenoide. Vamos a calcular el campo en el centro de la espira (r = 0) y el solenoide tiene n = 1000 vueltas/m, entonces:
B_{hilo} = 4 \cdot 10^{-7}
B_{espira} = 1.26 \cdot 10^{-6}
B_{bobina} = 1.26 \cdot 10^{-4}
Es decir, la bobina genera un campo 100 veces superior a la espira y 1000 veces mayor que el hilo, por lo que, para generar campos magnéticos intensos, se emplean bobinas u otras geometrías que suelen implicar cables enrollados, lo que aumenta la intensidad encerrada.
En comparación, el campo magnético de la Tierra varía entre [25 – 65] \cdot 10^{-6} T, por lo que situar unas pocas espiras juntas ya pueden superar a la Tierra, por ejemplo, moviendo las agujas de una brújula.

B_x = \frac{\mu_0 I \, r\,R}{4\pi (r^2 + R^2)^{3/2}}\int_{0}^{2\pi} cos \phi \, d\phi