Física Electromagnetismo Campo Eléctrico
Tabla de contenidos
Campo Eléctrico
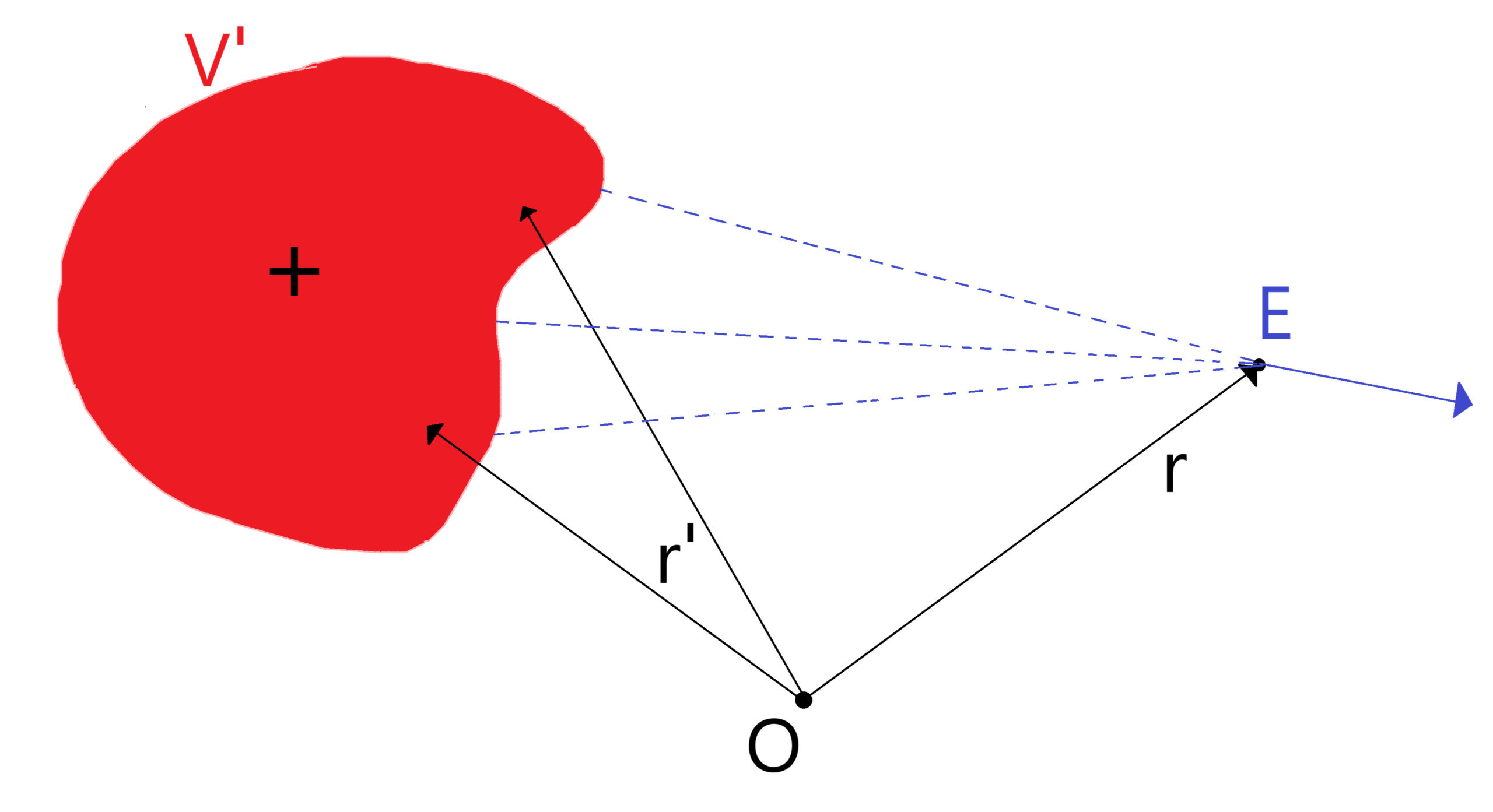
Es una región del espacio en la que existe una Fuerza Eléctrica creada por una (o más) cargas en el espacio y se define como la Fuerza que experimenta una carga Positiva en un punto del Campo Eléctrico por unidad de Carga:
\vec{E} \, = \, \int_{V'} \frac{\rho'(\vec{r}')(\vec{r}-\vec{r}')}{4\pi \epsilon_0 |\vec{r}-\vec{r}'|^3}
Donde \epsilon_0 es la constante dieléctrica del vacío (\epsilon_0 = 8.85\cdot 10^{-12} F/m \, o \, C^2/Nm^2 y las magnitudes con ‘ son de las fuentes y \vec{r} es la distancia desde el origen hasta el punto donde medimos el campo. |E|mide en Netwon por Culombio N \, / \, C o Voltio por metro V/m.
Para una carga puntual Q esta integral es muy sencilla llegando a que el campo a una distancia \vec{r} de la carga es:
\vec{E} = \frac{Q}{4\pi \epsilon_0 r^2} \hat{r}
Líneas de Campo:
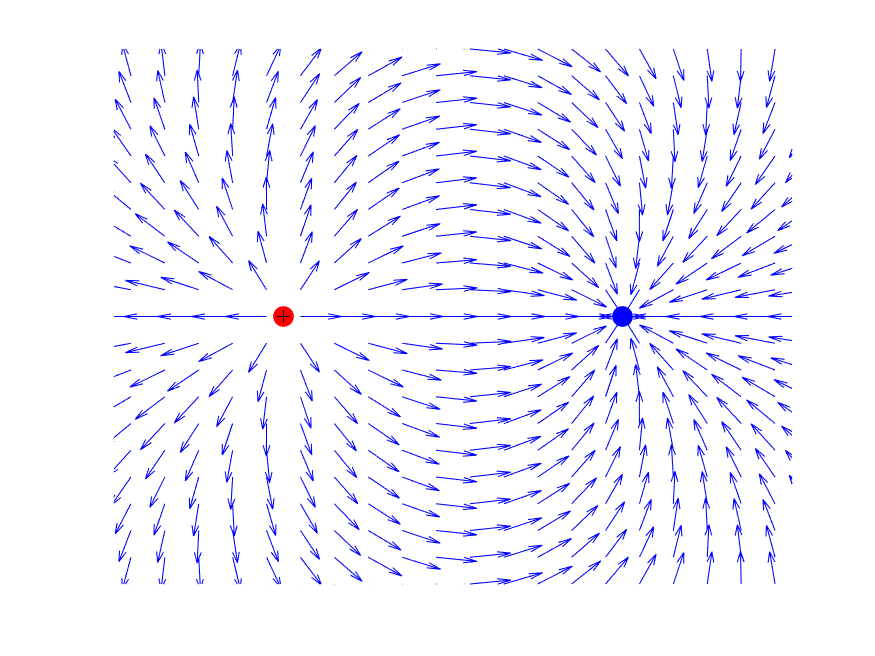
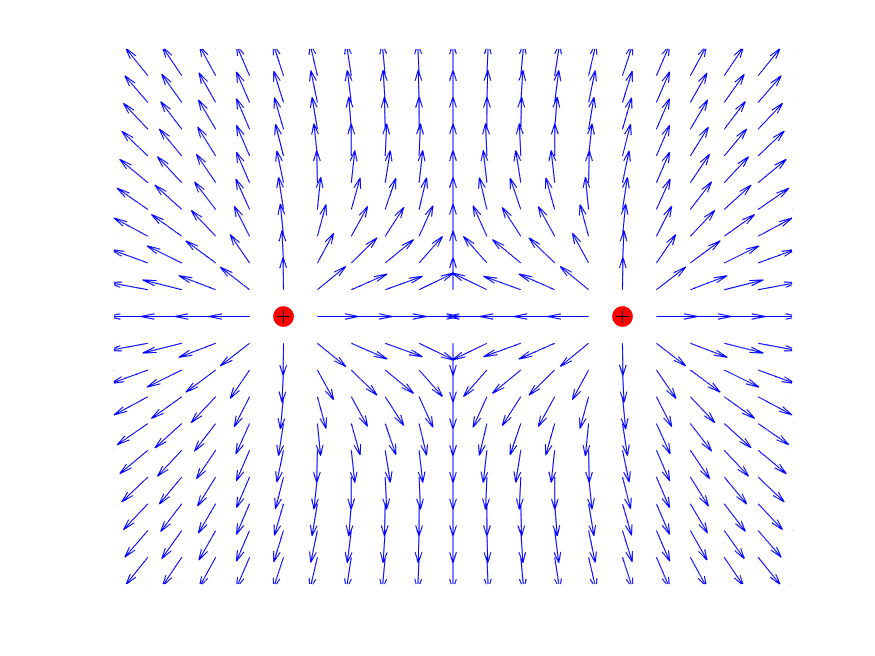
Es una representación del campo en el espacio. Las líneas representan la trayectoria que seguiría una carga positiva situada en un punto cualquiera manteniéndose las otras fijas. El número de líneas de campo representa la intensidad del campo. Las líneas nacen en las cargas positivas y mueren en las negativas de la siguiente manera:
Teorema de Gauss:
El Teorema de Gauss nos indica que el flujo de campo eléctrico, es decir, las líneas de campo que atraviesan una superficie son proporcionales a la carga encerrada por dicha superficie. Esto nos permite calcular el campo eléctrico en la superficie de un volúmen a partir de la carga dentro de ese volúmen:
\int_S \vec{E}\cdot d\vec{S} = \frac{Q_{encerrada}}{\epsilon_0}
Donde d\vec{S} denota un elemento de superficie con dirección normal a ésta. NOTA: esta fórmula es muy útil en situaciones de alta simetría, como esferas, líneas infinitas entre otros casos, si no hay alta simetría, es mejor resolver la integral.
Campo creado por una carga puntual
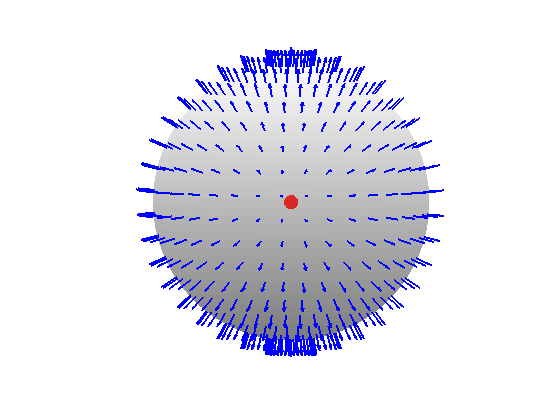
Hagamos un ejemplo: queremos calcular el campo creado por una carga puntual a una distancia r de ella. Si tomamos la esfera de radio r con carga Q en su interior de la imagen siguiente:
Podemos obtener que el campo es perpendicular en cada punto a la superficie de la esfera, es constante en módulo sobre ésta y que tiene dirección radial. Es decir,
\bf{\vec{E}\cdot d\vec{S} = E \, dS} \bf{\vec{E} = E \, \hat{r}}
Con esto, y sabiendo que la superficie de la esfera es 4\pi r^2, la integral resulta:
\int_{esfera}\vec{E}\cdot d\vec{S} = E \, S = E \, 4\pi r^2 = \frac{Q}{\epsilon_0}
E = \frac{Q}{4\pi \epsilon_0 \, r^2} \rightarrow \vec{E} = \frac{Q}{4\pi \epsilon_0 \, r^2} \, \hat{r}
Que es la fórmula que teníamos antes.
Campo creado por un hilo cargado infinito.
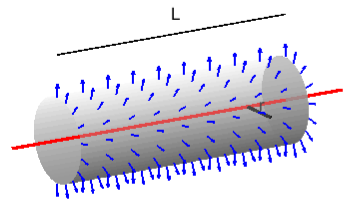
Para este caso, por simetría, vamos a elegir una corteza cilíndrica de radio r para medir el campo a esa distancia y con longitud L. De la imagen sacamos que el campo es, de nuevo, constante y perpendicular a la superficie y con dirección radial, sin embargo, hay que tener en cuentas las tapas del cilindro. Como el hilo es infinito, hay tanta carga a la izquierda como a la derecha, por lo que el campo que queda está orientado radialmente, así que:
\bf{\vec{E}\cdot d\vec{S}_{rollo} = E\, dS} \bf{\vec{E}\cdot d\vec{S}_{tapas} = 0}
Ahora, sabiendo que la superficie lateral del cilindro es S = 2\pi \, r \, L y que la carga encerrada por esa superficie es Q = \lambda \, L, podemos calcular la integral:
\int \vec{E}\cdot \, d\vec{S} = \int E \, dS = E \, S = \frac{\lambda \, L}{\epsilon_0}
E = \frac{\lambda}{2\pi \epsilon_0 \,r} \rightarrow \vec{E} = \frac{\lambda}{2\pi \epsilon_0 \, r}\, \hat{r}
Principio de Superposición
El campo eléctrico cumple el Principio de Superposición, es decir, que el campo total en un punto es la suma de todos los campos existentes en ese punto, por lo tanto:
\vec{E}_{T} \, = \, \vec{E}_{1} + \vec{E}_{2} + …
Campo Conservativo
El campo Eléctrico es un Campo Conservativo, es decir, que bajo su acción, los cuerpos conservan su Energía Mecánica y que, en una trayectoria cerrada, el Trabajo realizado por el campo es 0.
A continuación te dejo un pequeño simulador donde puedes crear cargas positivas y negativas (cambia el tipo dándole al botón) para crearlas toca la pantalla y si quieres darles una velocidad inicial, arrastra el ratón/dedo, cuanto más arrastres, mayor será la velocidad. También puedes fijar alguna carga si no quieres que se mueva activando el botón. Pulsa Lanzar para empezar y Reiniciar para eliminar todas las cargas.
Con este juego puedes comprobar el Teorema de Gauss, si fijas 4 cargas positivas juntas y lanzas una negativa libre, la fuerza será 4 veces superior a si hay una sola. También, si pones tantas cargas negativas como positivas muy cerca y fijas y lanzas una carga cualquiera , verás que, prácticamente, no sentirá fuerza.
Si tienes muy buen ojo y pulso puedes encontrar posiciones de equilibrio, colocando 2 cargas fijas positivas alejadas entre sí, si colocas una carga negativa justo en el medio, verás que no se mueve (en la realidad, como no es justo el medio se irá lentamente hacia una de las cargas).
Si consigues que una carga negativa orbite a una positiva que está fija has creado un átomo de hidrógeno como se pensaba que era según la mecánica clásica: un electrón ligero (se mueve) que orbita un protón masivo (no se mueve), siendo de igual carga pero de signo opuesto.
