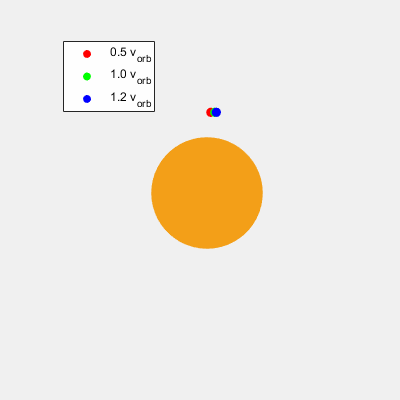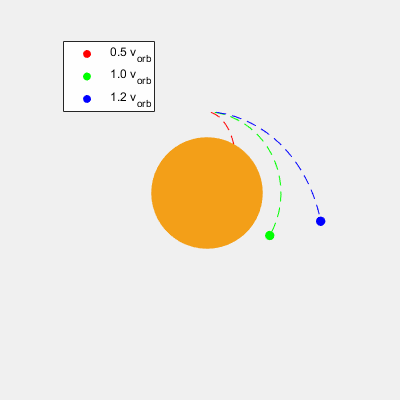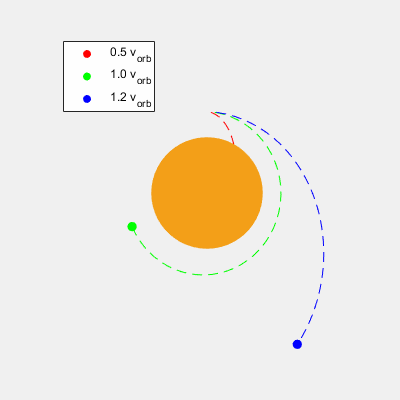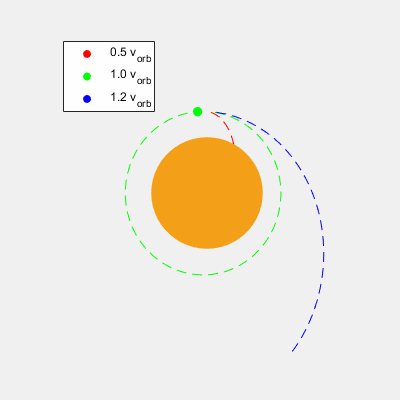
Velocidad de Órbita

Es la velocidad que debe llevar un cuerpo para orbitar a otro a una altura determinada sobre su superficie. Como podemos aproximar las órbitas a circulares, la distancia al centro y velocidad se mantendrá constante. Si el cuerpo está a una altura

h

sobre la superficie del cuerpo, se encuentra a una distancia

r \, = \, R + h

del centro del planeta grande. Sabiendo esto y la masa

M

del planeta grande:

$v_{orbita} \, = \, \sqrt{\frac{GM}{r}}$

Además, como es una órbita circular a velocidad constante, el satélite describe un MCU, por lo que:

$\omega \, = \, \frac{v}{r} \rightarrow T \, = \, \frac{2\pi r}{v}$

$T = \sqrt{\frac{4\pi^{2} r^{3}}{GM}}$

Que nos permite conocer el periodo de órbita del planeta.

Derivación de Fórmulas:

Estas fórmulas se obtienen directamente desde la Ley de Gravitación Universal y la Fuerza Centrípeta: Sabemos que el cuerpo describe un MCU, para lo cual es necesario que esté sujeto a una Fuerza Centrípeta, la cual es la Gravitatoria, pues no hay otra fuerza actuando sobre el cuerpo, entonces:

$F_{c} \, = \, F_{G} \rightarrow ma_{c} \, = \, \frac{GMm}{r^{2}}$

Sustitutendo en la fórmula

a_{c} \, = \, \frac{v^{2}}{r}

y simplificando las

m

r

$v^{2} \, = \, \frac{GM}{r}\rightarrow v \, = \, \sqrt{\frac{GM}{r}}$

En cambio, si sustituimos

a_{c} \, = \, \omega^{2}r

, obtenemos:

Tabla de contenidos