Al ser la Fuerza Gravitatoria una Fuerza Conservativa, podemos definir una Energía Potencial asociada a la fuerza como:

E_{p} \, = \, -\frac{GMm}{r}

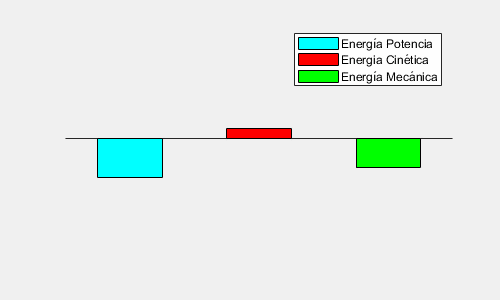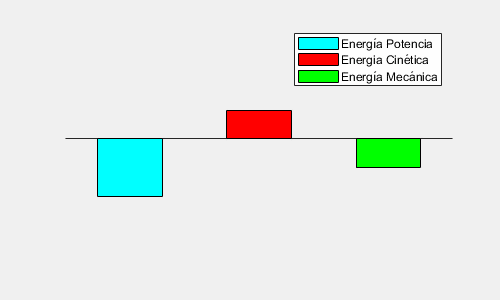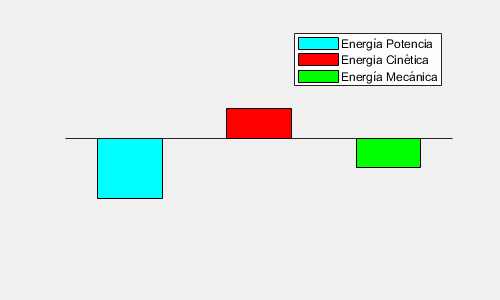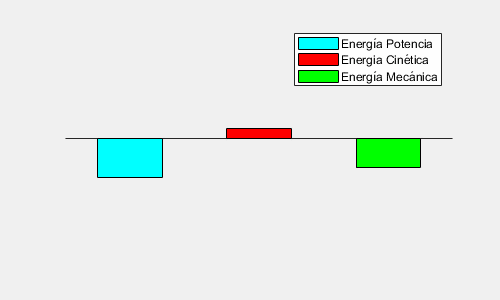
A partir de esta expresión podemos calcular la Energía Mecánica de un cuerpo en órbita:

E_{M} \, = \, E_{c} + E_{p} \, = \frac{1}{2}mv^{2} – \frac{GMm}{r}

Como v es la Velocidad de Órbita  que podemos calcular como v_{orb} = \sqrt{\frac{GM}{r}}, entonces:

E_{M} = \frac{GMm}{2r} – \frac{GMm}{r}

E_{M} = -\frac{GMm}{2r}

Además, esta Energía se conserva a lo largo de toda la órbita, pues la Fuerza Gravitatoria es Conservativa.