Física Electromagnetismo Potencial Eléctrico
Tabla de contenidos
Potencial Eléctrico
El potencial eléctrico, también llamado voltaje o tensión en circuitos, es una magnitud escalar que mide la energía potencial por unidad de carga en un punto del espacio. Se mide en voltios (V = J/C) y se define como:
V = \frac{E_p}{q}
La energía potencial eléctrica mide la energía que posee un cuerpo por estar inmerso en un campo eléctrico (ver Energía).
De manera similar que con el campo eléctrico, podemos calcular el potencial mediante una integral:
V = \int_{V'} \frac{\rho'(\vec{r}')}{4\pi \epsilon_0 |\vec{r}-\vec{r}'|}
Donde \epsilon_0 es la constante dieléctrica del vacío (\epsilon_0 = 8.85\cdot 10^{-12} F/m \, o \, C^2/Nm^2 )
Para el caso de una carga puntual Q tenemos que:
V = \frac{Q}{4\pi \epsilon_0 r}
Principio de Superposición.
El potencial eléctrico cumple el principio de superposición, es decir, el potencial total en un punto es la suma de todos los campos contribuyentes:
V_T = V_1 + V_2 + …
Relación con el campo eléctrico.
Tanto el campo como el potencial eléctrico pueden usarse para describir la misma situación, y al igual que en el caso del campo y potencial gravitatorio, se relacionan de la siguiente manera:
\vec{E}= -\nabla V = -(\frac{\partial V}{\partial x},\frac{\partial V}{\partial y},\frac{\partial{V}}{\partial z})
O, si invertimos esta relación:
V(x,y,z) = -(\int^x_{x_o} E_x dx + \int^y _{y_o} E_y dy + \int^z _{z_o} E_z dz) +C
Donde (x,y,z) es el punto donde medimos el potencial y (x_o, y_o,z_o) el punto donde hemos situado nuestro origen de potencial, es decir, que si lo elegimos correctamente (suele ser el infinito) nos eliminamos todas las constantes.
A través de estas relaciones, podemos calcular gran cantidad de cosas, como el campo eléctrico que circula por un cable sometido a un voltaje V, la diferencia de potencial entre las placas de un condensador entre otras muchas.
Superficies equipotenciales
Como es una magnitud escalar, podemos representarlo o mediante una escala de colores o a través de sus superficies equipotenciales:
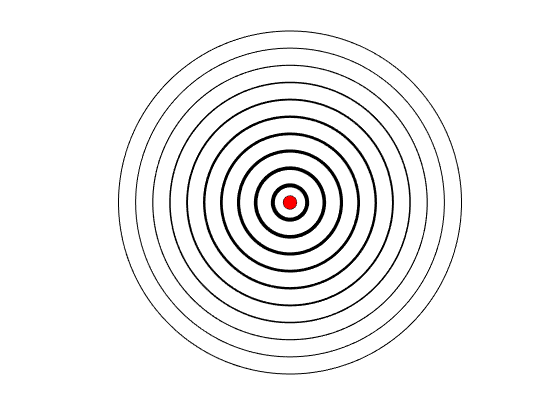
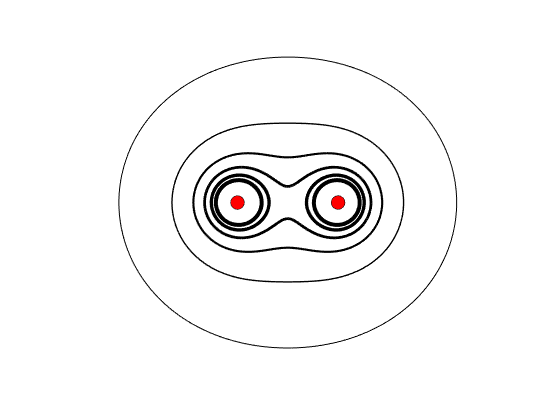
Estas superficies siguen el mismo principio que las isobaras del mapa del tiempo, es decir, las superficies (o líneas en 2D) son puntos donde el potencial es igual. El valor de estas líneas puede representarse a través de la anchura del trazo, como es este caso, donde las líneas más gruesas indican potenciales mayores o directamente etiquetando cada línea con un valor específico.
