Física Cinemática Sistemas de Coordenadas
Sistemas de Coordenadas
Tabla de contenidos
Es un conjunto de números a los que podemos asociar cada punto del espacio. Éstos números se determinan a partir del sistema de referencia.
Sistema de referencia:
Es un objeto, punto del espacio o conjunto de éstos que consideramos fijos (que no se mueven) desde los cuales estudiamos el movimiento de los cuerpos de alrededor. Al ser un sistema ortonormal, los vectores correspondientes a cada eje son perpendiculares entre sí y tienen módulo unidad:
Los sistemas de coordenadas suelen definirse mediante los ejes coordenados, un orígen y una serie de vectores que permiten dotar de un número (o varios) a un punto en el espacio.
Hay una gran cantidad de sistemas de coordenadas, pero en física solemos usar sistemas ortonormales, es decir, los ejes son perpendiculares entre sí, y los vectores que los definen tienen módulo 1. Pueden definirse infinidad de éstos, pero se dividen entre 2D y 3D
En 2D:
Coordenadas Cartesianas:
Son las más utilizadas, son los ejes X-Y que se ven en la mayoría de gráficas, no sólo en física, sino en prácticamente todos los campos En ellos los vectores unitarios que los definen son (\vec{x} ,\vec{y})/(\vec{i},\vec{j})/(\vec{e_{x}},\vec{e_{y}}) usados indistintamente. Son los que se utilizan en movimientos como MRU, MRUA o Tiro Parabólico
Los ejes coordenados X-Y reciben el nombre de abcisas y ordenadas respectivamente (o simplemente ejes x e y).
Para designar un punto, se utiliza el par de coordenadas (a,b), donde a representa el número de vectores \vec{x} que hacen falta para alcanzar esa posición, y b lo mismo pero con \vec{y}. Por ejemplo, el punto (2,1) significa que hacen falta 2 vectores \vec{x} y 1 vector \vec{y} para llegar a ese punto. En el siguiente gráfico interactivo puedes ver esto. Mueve el punto azul para ver cómo cambian las coordenadas, vectores y ángulos.
Proyección de vectores:
En primer lugar, denotaremos \vec{v_{x}} y \vec{v_{y}} a las componentes del vector \vec{v} sobre los ejes X e Y respectivamente. Además, tomaremos el ángulo \theta como el ángulo entre el vector \vec{v} y el eje X. También tomaremos \varphi como su complementario.
También cabe recordar que para conocer el módulo de un vector v=|\vec{v}| podemos aplicar el Teorema de Pitágoras:
v=\sqrt{v_{x}^{2}+v_{y}^{2}}
- Si conocemos \vec{v} y un ángulo:
\vec{v_{x}}=v \, cos\theta \, \vec{i} \ = \ v \sin\varphi \, \vec{i}
\vec{v_{y}}=v \, sin\theta \, \vec{j} \ = \ v \cos\varphi \, \vec{j}
- Si conocemos \vec{v} y una de sus proyecciones:
\vec{v_{x}}=\vec{v}-\vec{v_{y}}
\vec{v_{y}}=\vec{v}-\vec{v_{x}}
Coordenadas Polares:
Es otro sistema de coordenadas muy utilizado, se emplea para describir figuras que son circulares o tienen algún tipo de simetría radial, como elipses (óvalos) o movimientos que tienen trayectoria circular como el MCU. En ellos los ejes son el eje radial y el angular, se suele utilizar la letra r para designar al radial y una letra griega (\theta / \varphi / \alpha …) para el angular.
Para designar un punto en este sistema es muy sencillo, en primer lugar se encuentra la distancia de este punto al origen O, después se encuentra el ángulo al que éste se encuentra respecto al ángulo 0. En el siguiente gráfico interactivo puedes jugar con esto:
Como puedes ver si pones el punto en dos sitios simétricos, r no cambia de signo, sólo cambia el ángulo, por lo que puntos que se encuentran a la misma distancia del origen tendrán la misma coordenada r. ¿Y qué es el conjunto de los puntos que están a la misma distancia de un centro? Una circunferencia, la cual es mucho más fácil de definir mediante coordenadas polares.
En cartesianas, una circunferencia de radio a son los puntos que satisfacen la ecuación:
x^{2}+y^{2}=a^{2}
Que no es muy práctica, pues hay que estar probando para encontrar los puntos. Sin embargo, usando coordenadas polares, los puntos tienen que satisfacer la ecuación:
r=a
Además el cambio de coordenadas de polares a cartesianas es muy sencillo:
x=r \, cos \, \theta
y=r \, sin \, \theta
En 3D:
Coordenadas Cartesianas:
- Con varios gráficos: Es decir, hacer un gráfico X-Y, otro X-Z y otro Y-Z, que nos permite visualizar los 3 ejes, pero en gráficas diferentes.
- Un gráfico en 3D: Pueden hacerse figuras en falso 3D en papel añadiendo sombras o estilos de línea que indiquen profundidad, sin embargo, éstos dibujos son más difíciles de realizar. También pueden hacerse gráficos interactivos mediante herramientas en ordenador como geogebra, matlab…
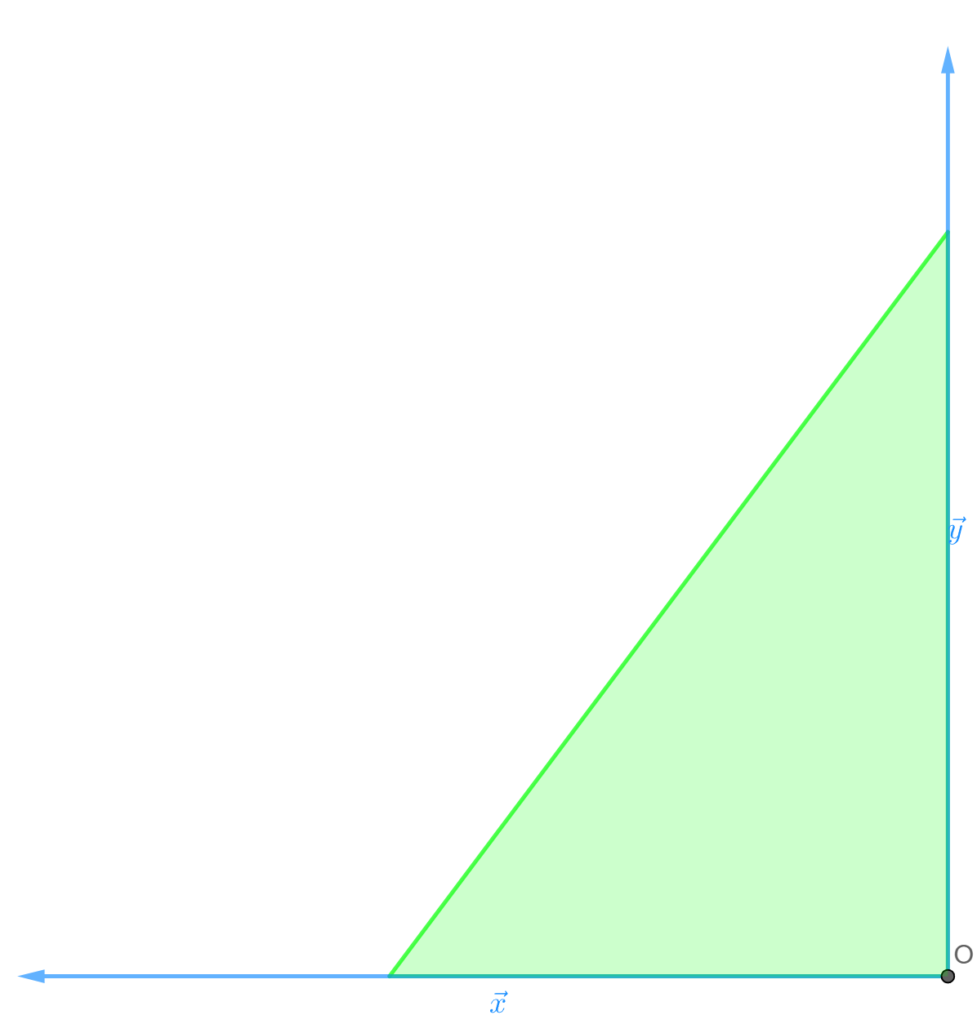
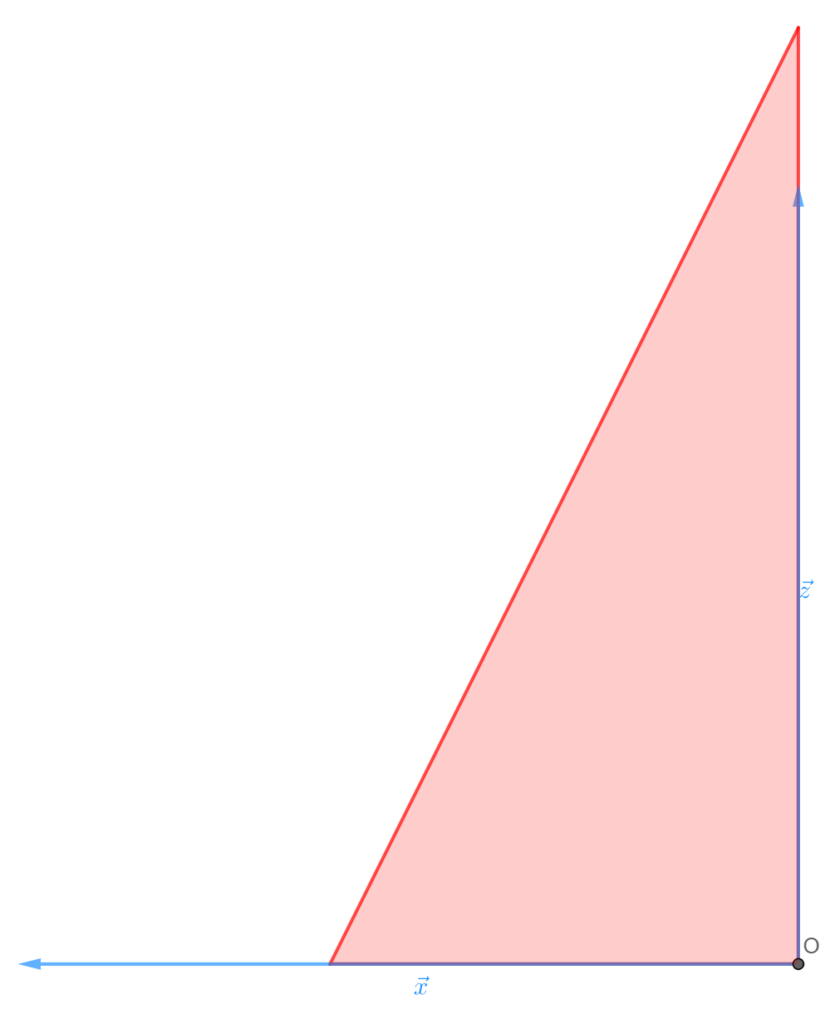
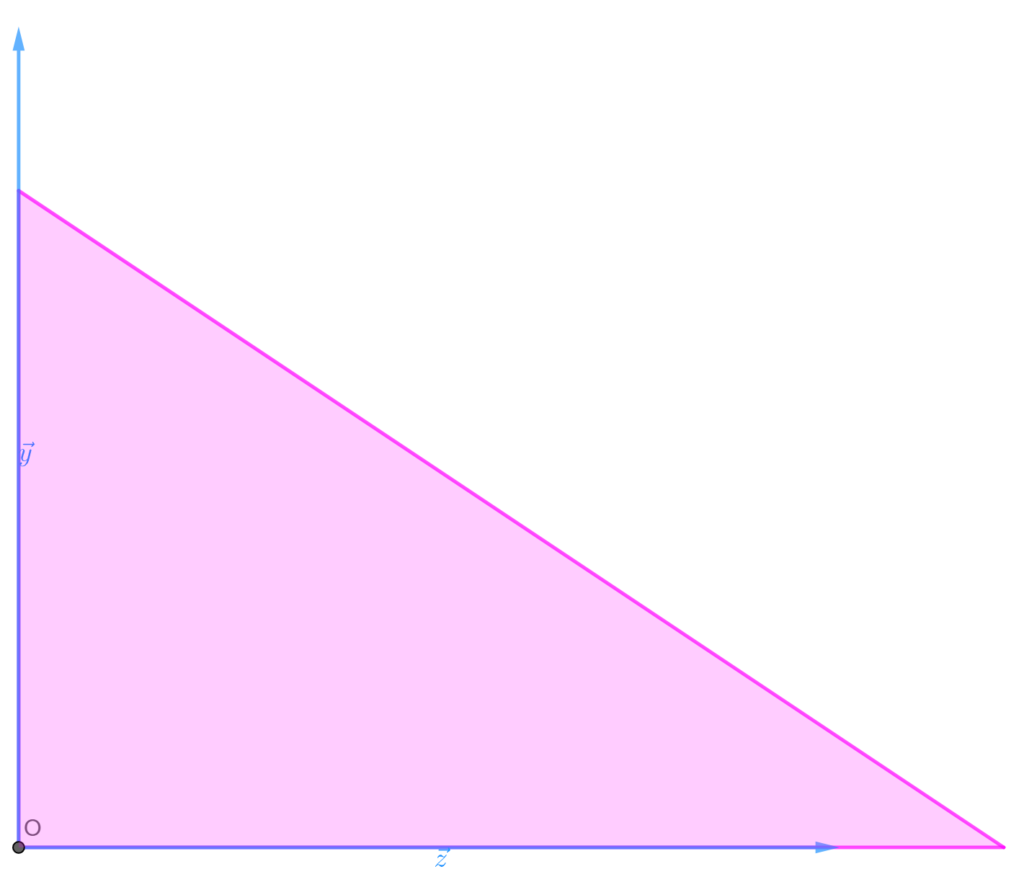
Proyección de vectores:
Como se ve en la gráfica, el ángulo \theta corresponde al ángulo que forma \vec{v} con el eje Z, y \varphi el ángulo de la proyección de \vec{v} sobre el plano X-Y.
Para conseguir las proyecciones, seguimos los siguientes pasos:
- Proyectamos \vec{v} sobre el eje Z y sobre el plano X-Y de la siguiente manera:
v_{z}=v \, cos\theta
v_{x-y}=v \, sin\theta
- Con v_{x-y}, lo proyectamos sobre los ejes X e Y:
v_{x}=v_{x-y}cos \varphi
v_{y}=v_{x-y}sin\varphi
Todo esto, nos da la proyección de \vec{v} sobre los ejes X-Y-Z:
\vec{v_{x}}=v \, sin \theta \, cos \varphi \ \vec{i}
\vec{v_{y}}=v \, sin \theta \, sin \varphi \ \vec{j}
\vec{v_{x}}=v \, cos \theta \ \vec{k}
Coordenadas Cilíndricas:
Son iguales que las polares, pero añadiendo una tercera componente, es decir, para definir un punto, hay que dar la distancia del punto al origen r, el ángulo respecto a uno de los ejes \theta y la altura a la que se encuentra el punto respecto al plano del ángulo z:
De esta manera, las componentes del vector sería: (r,\theta,h). Y para proyectarlas en cartesianas, basta con calcular solamente (r \, cos\theta, r \, sin\theta, h).
Este sistema de coordenadas se emplea en menor medida que las esféricas (a continuación), pero son más útiles para describir ciertas figuras como cilindros o circunferencias a una altura dada.
