Propagación de Ondas
Las ondas son transferencias de energía sin desplazar materia, es decir, un onda se propaga por el medio, su posición cambia con el tiempo, por lo que podemos asociarle una velocidad \vec{v}.
La velocidad con la que se propaga una onda puede conseguirse desde la Ecuación de Onda, pero ésta depende del tipo de onda y del medio en la que ésta se propaga, por ejemplo, la luz se desplaza más despacio por el agua que en el vacío.
Sin embargo, podemos conocer la velocidad de propagación de una onda (periódica) conociendo los Elementos de una Onda, en concreto, su Longitud de Onda \lambda (o el número de onda k) y su Frecuencia Angular \omega (o su Periodo T/Frecuencia f).
Como \lambda es la distancia entre dos puntos consecutivos en fase y T el tiempo que tarda la onda en recorrer una longitud de fase, podemos calcular la Velocidad de Propagación de la onda v como:
v \, = \, \frac{\lambda}{T} \, = \, \lambda f,\ \ [v] \, = \, m/s
Que no depende del tiempo, es decir, la onda realiza un MRU, mientras que las partículas del medio por el que se propaga realizan un MAS.
Transmisión de Ondas
Las ondas en su recorrido a través de un medio puede encontrase con otro medio diferente, en este momento, la onda penetrará en el segundo medio y, en función de la Velocidad de Propagación del primer medio y del segundo (v_{1} \ y \ v_{2}), sucederán diferentes cosas:
Cuando llega a la superficie que separa los medios, la onda tiene una Amplitud y Número de Onda iniciales A_{i} \ k_{i}. Al penetrar en el medio, una parte de la onda lo atravesará y otra parte será reflejada, formándose dos nuevas ondas, una de Transmisión (T) y otra Reflejada (R), cuyas amplitudes son:
A_{T} \, = \ \frac{2k_{i}}{k_{i}+k_{2}}A_{i} \, = \, \frac{2v_{1}}{v_{1}+v_{2}}A_{i}
A_{R} = \frac{k_{i} – k_{2}}{k_{i} + k_{2}}A_{i} = \frac{v_{1} – v_{2}}{v_{1} + v_{2}}A_{i}
y_{i}(x,t) \, = \, A_{1} sin (k_{1} x \, – \, \omega t)
y_{R}(x,t) = -A_{R} sin (-k_{1} x+\omega t)
y_{T}(x,t) \, = \, A_{T} sin (k_{2} x \, – \, \omega t)
Cabe recordar que la Frecuencia f (y, por tanto \omega y T) de la onda no varían al cambiar de medio.
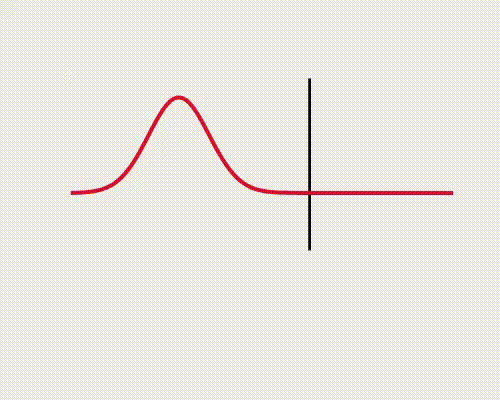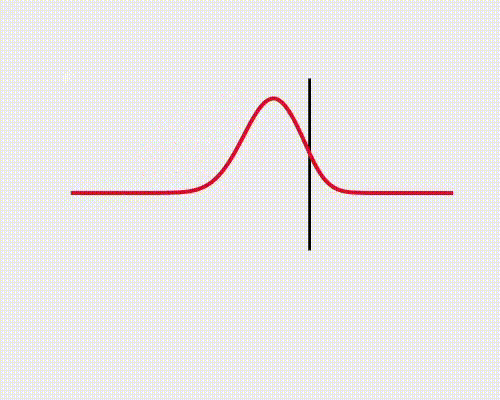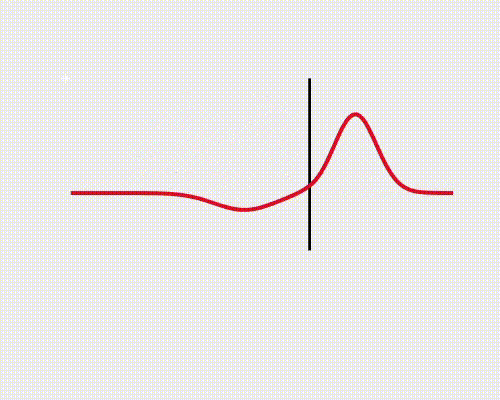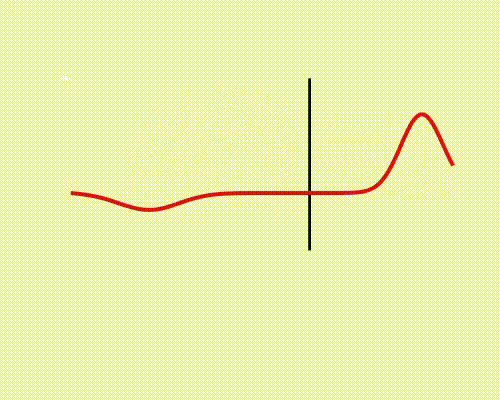
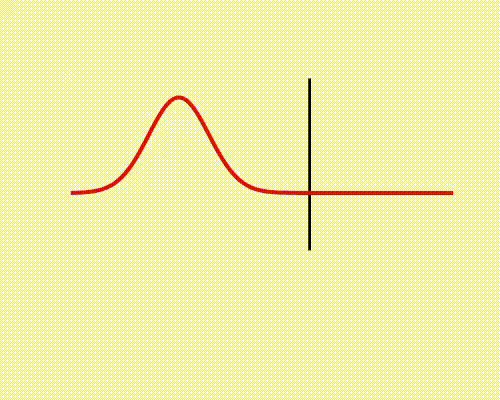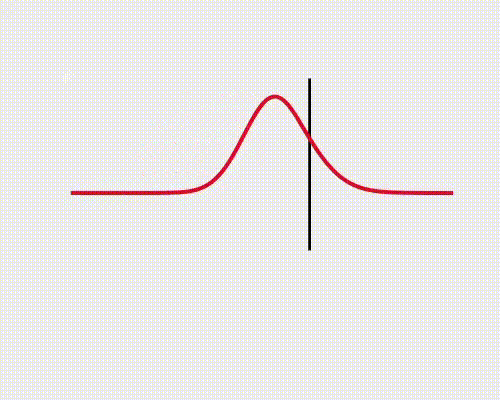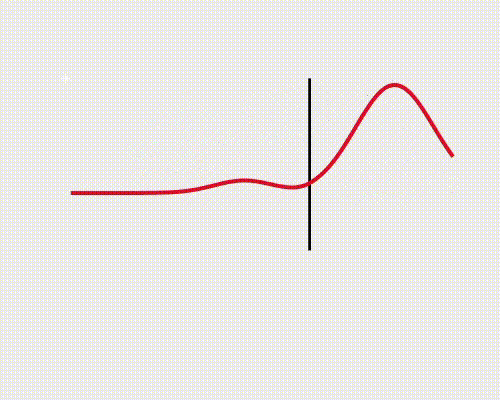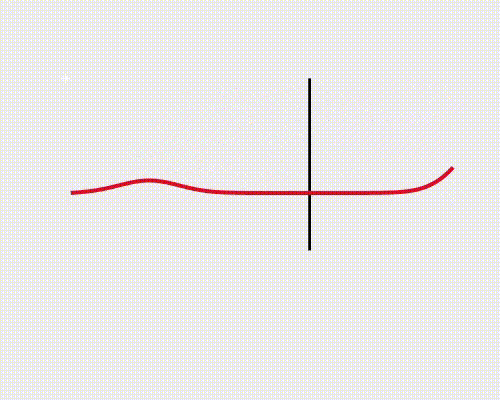
La onda de reflexión puede invertirse, lo cual depende de la velocidad de propagación de cada medio, pudiendo definir un Coeficiente de Reflexión:
r \, = \, \frac{A_{R}}{A_{i}} \, = \, \frac{v_{2} \, – \, v_{1}}{v_{2} \, + \, v_{1}}
- Si v_{2} \, < \, v_{1}, \, r \, < \, 0, la onda se invierte.
- Si v_{2} \, > \, v_{1}, \, r \, > \, 0, la onda no se invierte.