Interferencia de Ondas
Cuando dos o más ondas se encuentran en un mismo punto éstas interfieren entre sí, sumándose sus amplitudes. Sin embargo, tras encontrarse, cada onda sigue su propio camino:
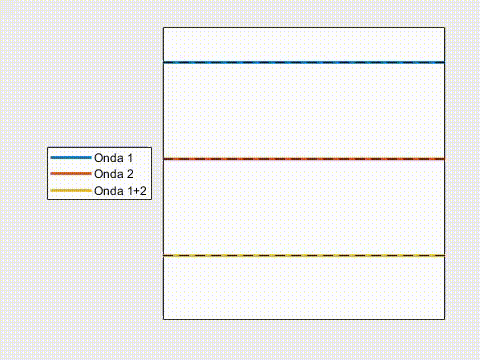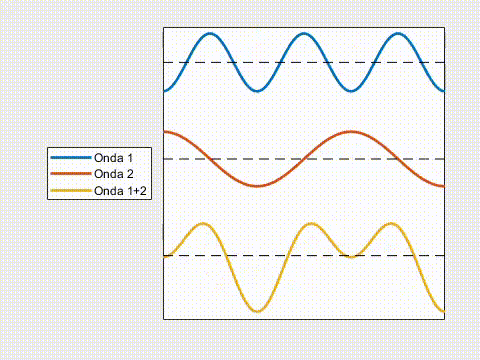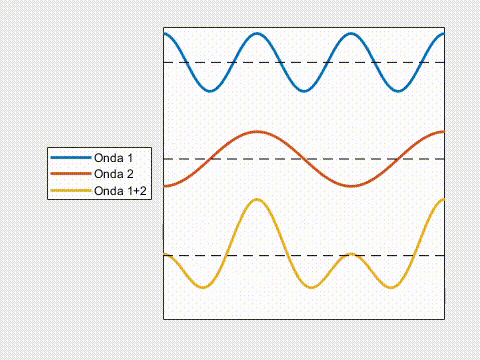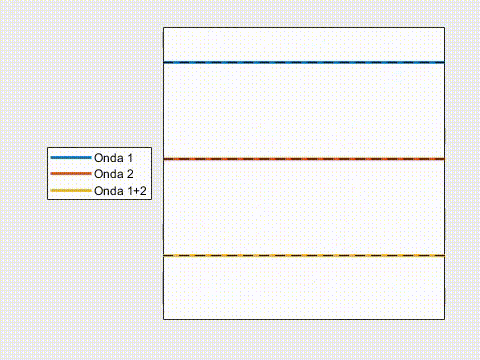
Como puedes ver, la onda resultante puede ser mayor que las originales o menor que éstas, es decir, que la interferencia puede ser constructiva (si son del mismo signo) o destructiva (si son de signos opuestos).
- Si las ondas llegan en igual fase (\phi = 0, 2\pi, 4\pi…), se trata de interferencia constructiva máxima donde A_{1,max} \, + \, A_{2,max} \, = \, A_{3}.
- Si llegan en oposición de fase (\phi \, = \, \pi, 3\pi, 5\pi…), interferencia destructiva máxima y A_{1,max} \, – \, A_{2,max} \, = \, A_{3}.
Pulsaciones y Batidos
Si tenemos dos ondas de frecuencias f_{1} y f_{2} muy cercanas entre sí (pero no iguales), se oirá como una única onda con la frecuencia promedio (f \, = \, \frac{f_{1} \, + \, f_{2}}{2}) cuya amplitud está modulada por la onda de batido, cuya frecuencia es la diferencia entre las ondas originales (f_{B} \, = \, |f_{1} – f_{2}|). Obteniéndose una onda de batido de la forma \bf{y_{B} \, = \, A cos(\pi \, f_{B} t)} y una modulada de la forma \bf{y \, = \, A cos(\pi \, f_{B} t)sin(2\pi f t)}.
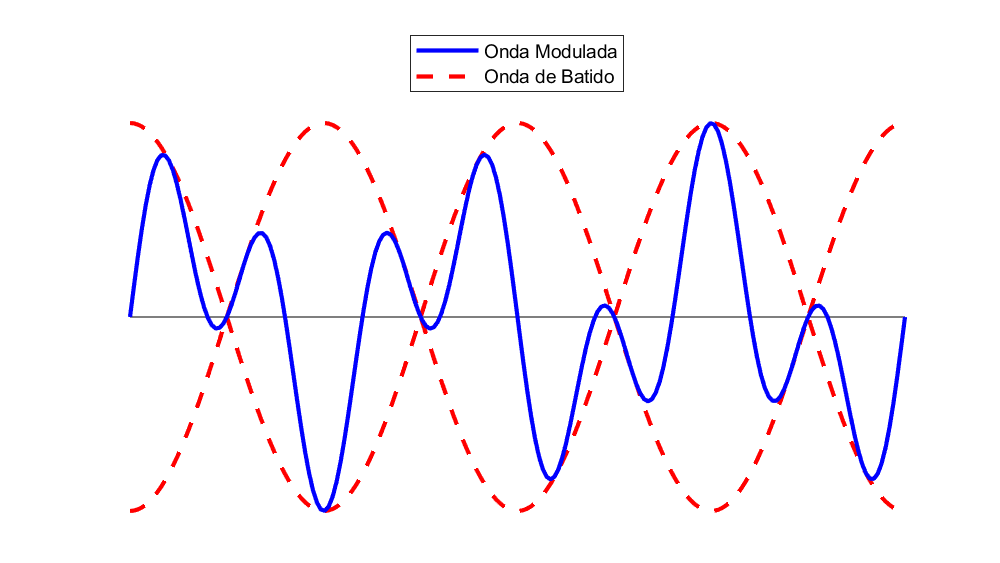
Onda de batimento entre dos ondas de frecuencia 400 Hz y 399 Hz
