Permite conocer la amplitud de una onda relacionando derivadas parciales temporales y espaciales:

\frac{\partial^{2} y}{\partial x^{2}} \, = \, \frac{1}{v^{2}}\frac{\partial^{2}y}{dt^{2}}

Donde y es la amplitud de la onda y v es la velocidad de propagación de la onda, es decir, la velocidad con la que se mueve la onda para un medio en concreto. Ésta ecuación puede convertirse en un sistema de ecuaciones diferenciales de segundo orden y resolverse, lo que, añadiendo ciertas condiciones iniciales y de contorno, nos da el siguiente resultado

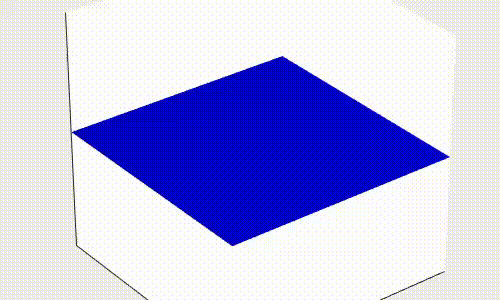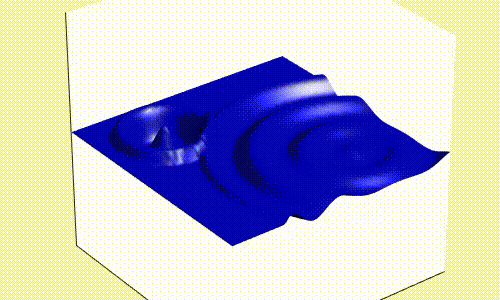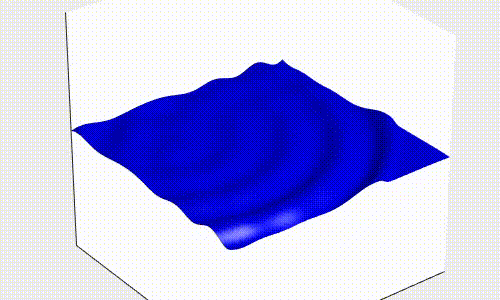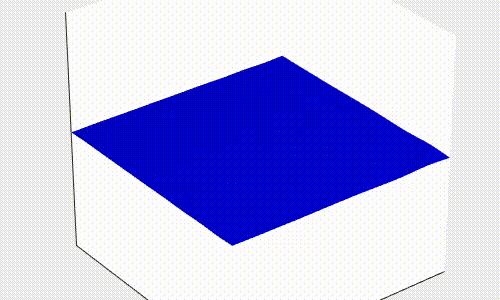
Como puedes ver, esta onda se parece mucho a una ola del mar, comportándose de manera similar a ésta.