Tabla de contenidos
Ondas Electromagnéticas
Las Ondas Electromagnéticas son perturbaciones del campo magnético y eléctrico que se propagan en el tiempo y el espacio. Siguiendo las ecuaciones de Maxwell, un campo eléctrico cambiante en el tiempo genera un campo magnético cambiante en el tiempo, que genera un campo eléctrico que cambia en el tiempo, retroalimentándose y, así, propagarse.
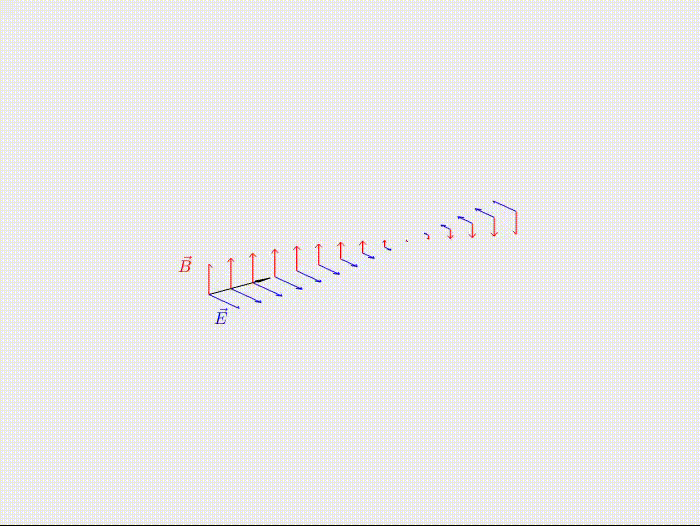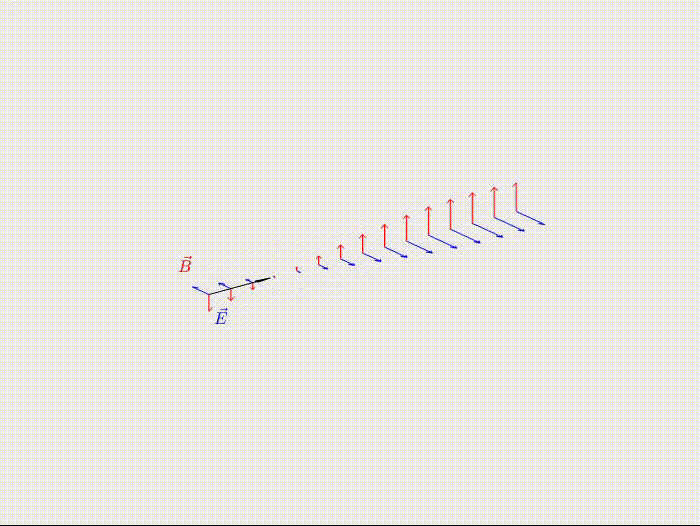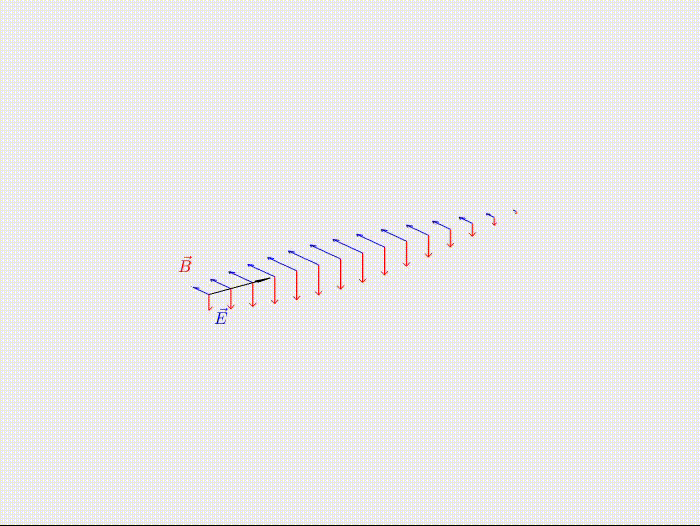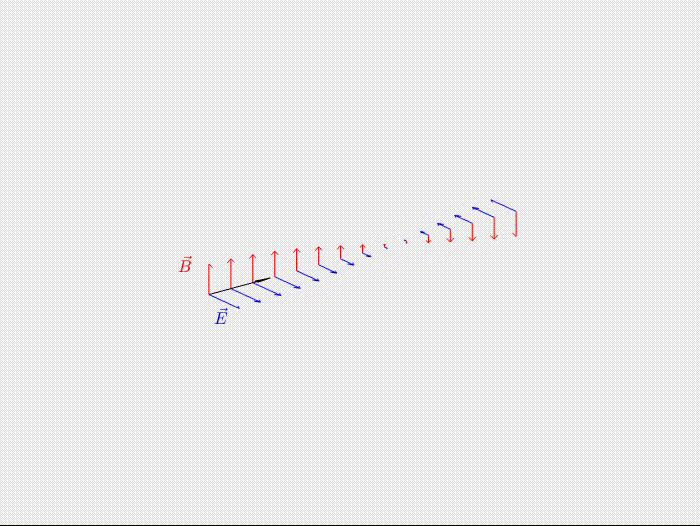
Son distintas a las ondas materiales como el sonido o las olas, no necesitan de un medio para propagarse (en el espacio no se oye pero sí se ve), pero siguen transportando energía.
Hay de muchas formas y muy complejas, pero todas pueden descomponerse como suma de ondas armónicas que están caracterizadas de la siguiente manera:
\vec{E} = \vec{E}_o \, cos(\vec{k}\cdot \vec{z} – \omega \, t) \ \ \ \ \vec{B} = \vec{B}_o \, cos(\vec{k}\cdot \vec{z} – \omega \, t + \phi)
Donde \vec{E}_o y \vec{B}_o son las amplitudes del campo eléctrico y magnético, respectivamente (con módulo, dirección y sentido), \vec{k} es el vector de onda, cuyo módulo indica cuántas oscilaciones hay por metro y su dirección y sentido indican hacia dónde se propaga la onda, \omega es la frecuencia angular, cuántas oscilaciones hay por segundo y \phi es el desfase entre el campo eléctrico y el magnético.
Para ondas planas (el campo eléctrico y magnético están localizados en un mismo plano) se cumplen las siguientes propiedades:
- \bf{\vec{E}} y \bf{\vec{B}} son perpendiculares a \vec{k}, es decir, no hay campo en la dirección de propagación.
- \bf{|E_o| = c |B_o|}, con c la velocidad de la luz (en el vacío c = 3\cdot 10^8m/s).
- \bf{\hat{E}\times \hat{B} = \hat{k}}, podemos obtener la dirección de \vec{k} a través de \vec{E} y \vec{B}.
- \bf{|k| = \frac{\omega}{c} = \frac{2\pi}{\lambda}}, con \lambda la longitud de onda (cuánto recorre la onda en una oscilación). Podemos calcular así el módulo del vector de onda.
Pongamos, por ejemplo, una onda electromagnética que se propaga en el vacío en dirección +z, cuya amplitud del campo eléctrico es \vec{E}_o = 1 \hat{x} V/m y tiene una frecuencia de 1 GHz.
La amplitud del campo magnético podemos calcularla a partir de las relaciones siguientes:
- \hat{E} \times \hat{B} = \hat{k} \rightarrow \hat{k} \times \hat{E}= \hat{B} \rightarrow \hat{z} \times \hat{x} = \begin{vmatrix} x & y & z \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{vmatrix} = \hat{y} que nos da su dirección.
- |B| = \frac{|E|}{c} = \frac{1}{3\cdot 10^8} = 3.33 \cdot 10^{-9} T, que nos da su módulo.
A partir de la frecuencia f = 1 GHz , podemos obtener la frecuencia angular \omega = 2\pi \, f = 2\pi \cdot 10^9 rad/s y el módulo del vector de onda |k| = \frac{\omega}{c} = \frac{2\pi \cdot 10^9}{3 \cdot 10^8} = 21 rad/m. \vec{k} \cdot \vec{r} = 21z. En el vacío no hay desfase entre los campos, así que \phi = 0, pudiendo calcular entonces los campos: