El momento lineal, momento, ímpetu o cantidad de movimiento \vec{p}, es una magnitud vectorial definida como el producto de la masa m por la velocidad \vec{v} de un cuerpo.

\vec{p} \, = \, m \vec{v} \ \ [p] \, =kg \, m/s

Si no hay fuerzas externas actuando sobre el sistema (o la neta total es 0), el momento lineal se conserva, es decir:

\vec{p}_{o} \, = \, \vec{p}_{f}

Esto nos permite describir las colisiones entre 2 o más cuerpos. Los choques se dividen en 2 tipos:

Choques Elásticos:

 En ellos se conserva tanto el momento como la Energía Cinética. Son los que ocurren, por ejemplo, con las bolas de billar:

\vec{p}_{o} \, = \, \vec{p}_{v}, \ \ E_{c,o} \, = \, E_{c,f}

p_{o}=1\cdot 2 + 2\cdot 0 \, = \, p_{f}= 1\cdot (-2/3) + 2\cdot 4/3 \, = \, 2 \, kg \, m/s

E_{c,o}=\frac{1}{2}\cdot 1 \cdot 2^{2} + \frac{1}{2}\cdot 2 \cdot 0^{2} \, = \, E_{c,f}=\frac{1}{2}\cdot 1 \cdot (2/3)^{2} + \frac{1}{2} \cdot 2 \cdot (4/3)^{2} \, = \, 2 \, J

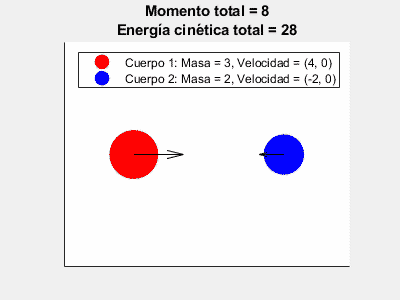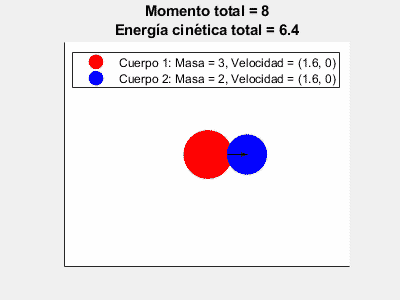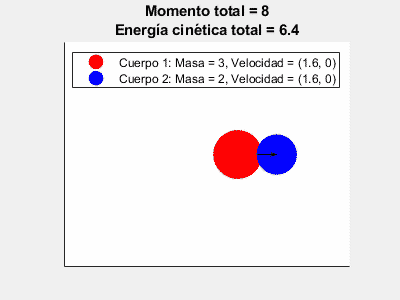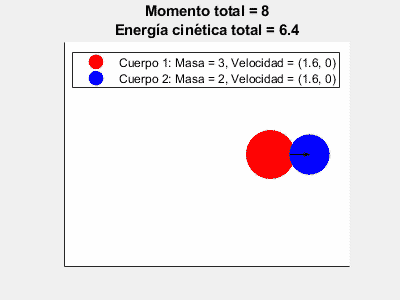
Choques Inelásticos:

En ellos sólo se conserva el momento lineal, no la Energía Cinética, la cual se disipa en otras formas de energía (principalmente calor). Estos son, principalmente, los choques donde los cuerpos acaban unidos entre sí:

\vec{p}_{o} \, = \, \vec{p}_{f}, \ \ E_{c,o} \, \neq \, E_{c,f}

Relación del Momento Lineal con las Fuerzas.

A través del Momento Lineal y su conservación, podemos derivar todas las leyes de Newton:

• Primera Ley de Newton: es consecuencia directa de la conservación del Momento Lineal, si no hay ninguna fuerza actúa sobre un cuerpo, conservará su Momento por lo que mantendrá un MRU.
• Segunda Ley de Newton: que define Fuerza como el cambio temporal del momento lineal (\vec{F} \, = \, \frac{d\vec{p}}{dt})
• Tercera Ley de Newton: también consecuencia del Momento Lineal. De la Segunda Ley hemos sacado que la Fuerza es un intercambio de Momento, es decir, que un cuerpo le «da» momento a otro, por lo que el que cede debe perder, siendo así que el cambio total de Momento Lineal 0. Que un cuerpo de momento y otro reciba es equivalente a que ambos cuerpos realicen entre sí una fuerza igual y opuesta.