Tabla de contenidos
Momento Angular
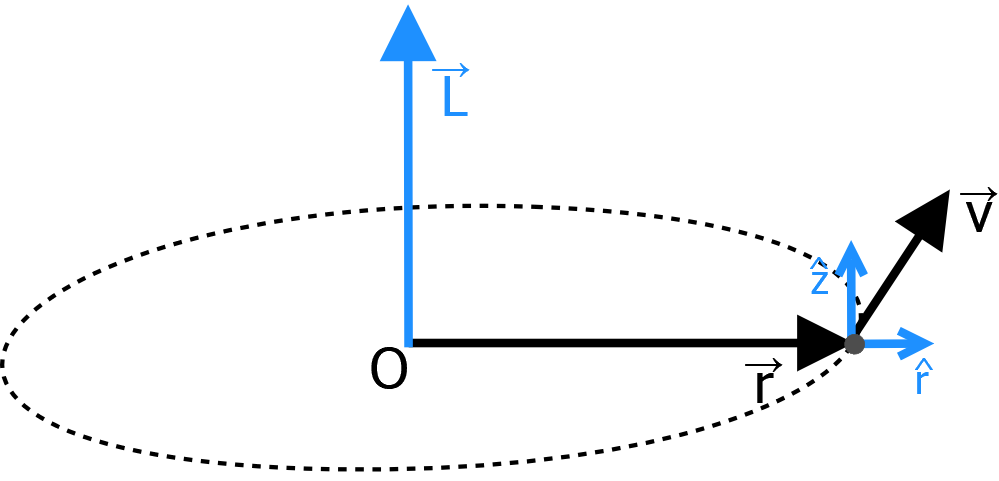
El momento angular o cinético \vec{L} respecto a un punto O de un cuerpo se define como el producto vectorial del vector \vec{r} que une el cuerpo con el punto O y el momento lineal \vec{p} del cuerpo:
\vec{L} \, = \, \vec{r} \times \vec{p} \, = \, m \, \vec{r}\times \vec{v}=m \, r^{2} \, \vec{\omega}
|\vec{L}| \, = \, kg \, m^{2}/s
Torque o Momento
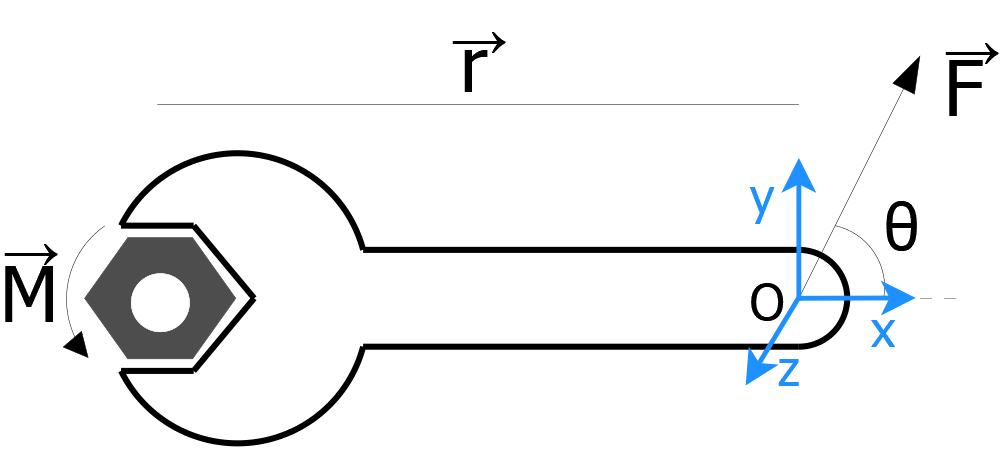
El torque o momento \tau \ / \ M respecto a un punto permite conocer cómo cambia el momento angular respecto a ese mismo punto en el tiempo debido a una fuerza externa:
\vec{\tau} \, = \, \vec{r}\times\vec{F}
\vec{\tau} \, = \, \frac{d\vec{L}}{dt} \, = \, \frac{\vec{r}\times\vec{p}}{dt} \, = \, \vec{r}\times\vec{F}
Fuerzas Centrales:
Hemos visto que cuanto mayor sea el Torque, más rápido cambiará el Momento Cinético, lo que provoca que el móvil describa un MCUA, puesto que su velocidad angular cambia en el tiempo.
Pero ¿Qué pasa si el Torque es 0?, esto hace que la Aceleración Angular sea 0. Es decir, el cuerpo siempre gira con la misma velocidad angular \vec{\omega}, es decir, describe un MCU. Esto puede pasar por 2 causas:
- \vec{r}=0, es decir, que el punto sobre el que aplica la Fuerza es el mismo punto donde se encuentra el cuerpo. Esto provoca que el cuerpo no rote, sólo que sea empujado normalmente.
- Que \vec{r} sea paralelo a \vec{F}, esto provoca que el producto escalar sea 0. En este caso a \vec{F} se la denomina Fuerza Central, puesto que apunta al centro del eje de giro. Un ejemplo de fuerza central es la Fuerza Gravitatoria, lo que hace que los planetas conserven el Momento Angular.
Si el Momento Angular se conserva, significa que:
\vec{L} \, = \, cte. \rightarrow r_{o} \, v_{o} \, = \, r_{f} \, v_{f}
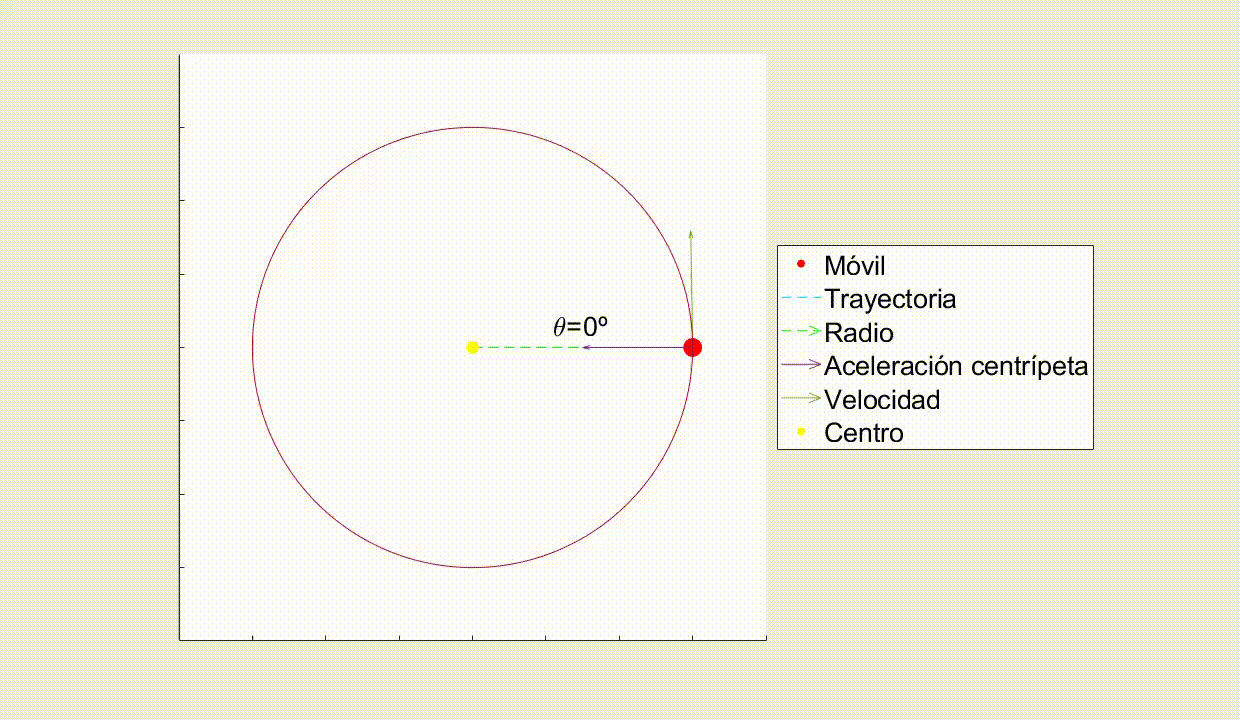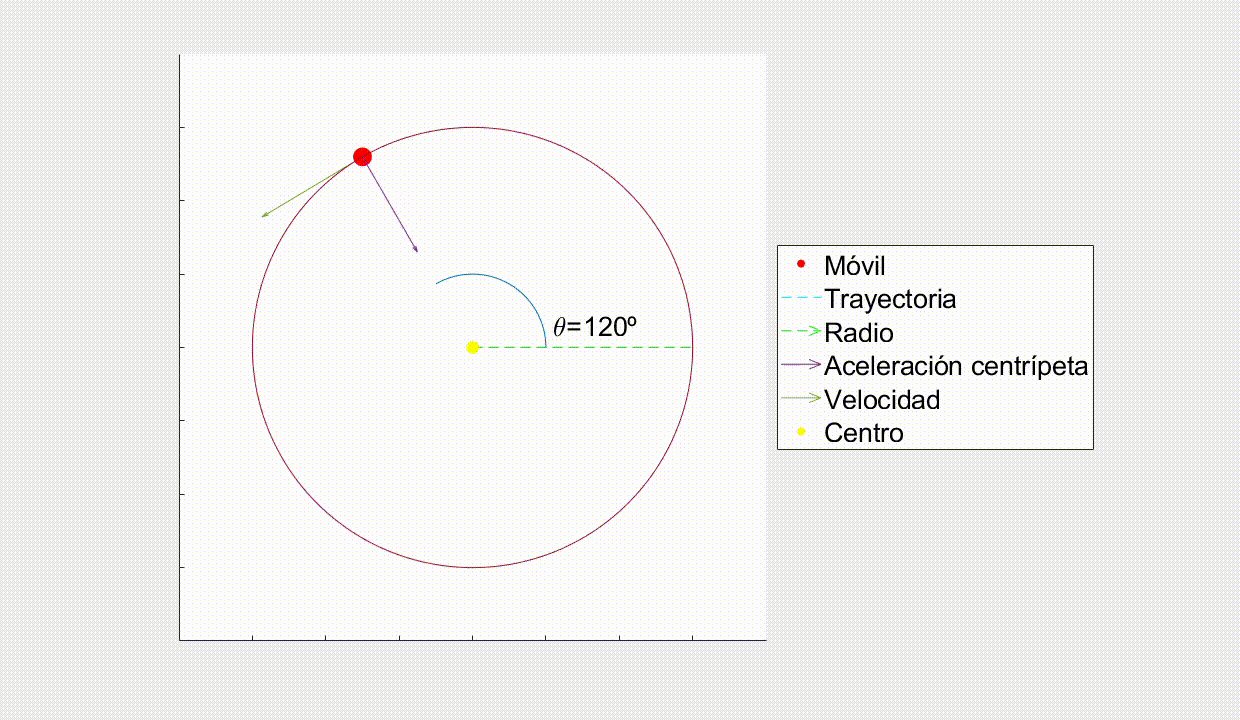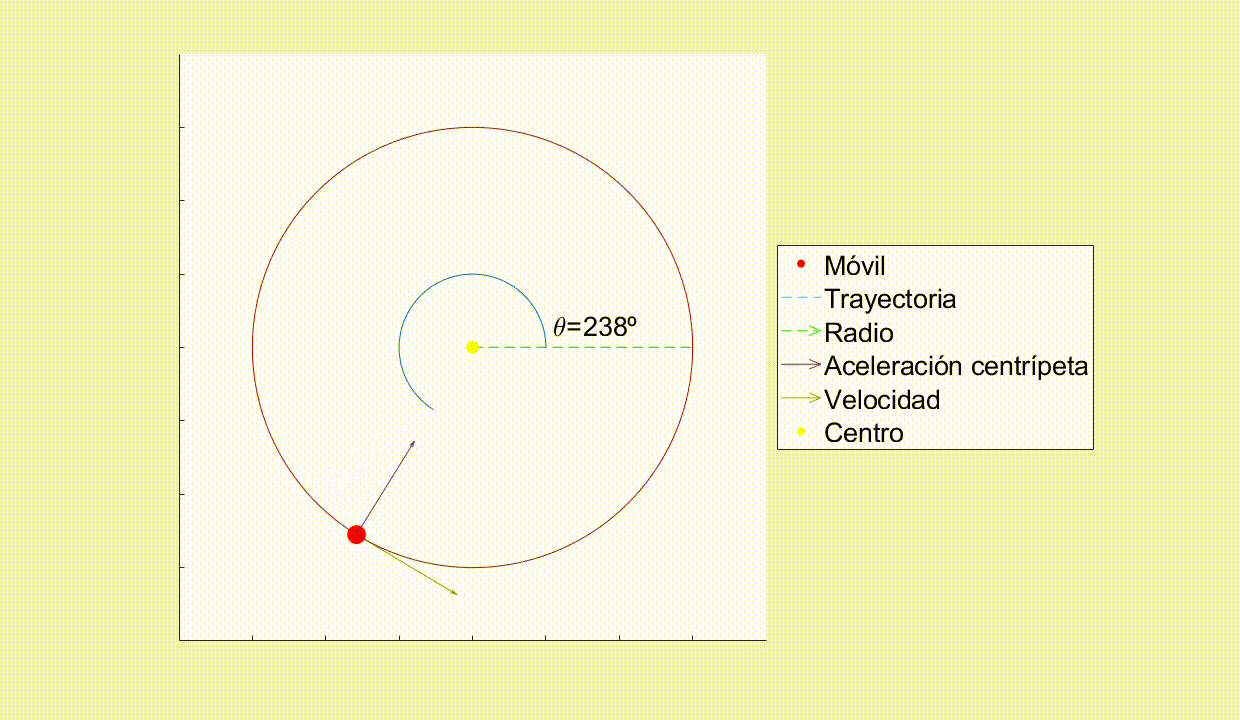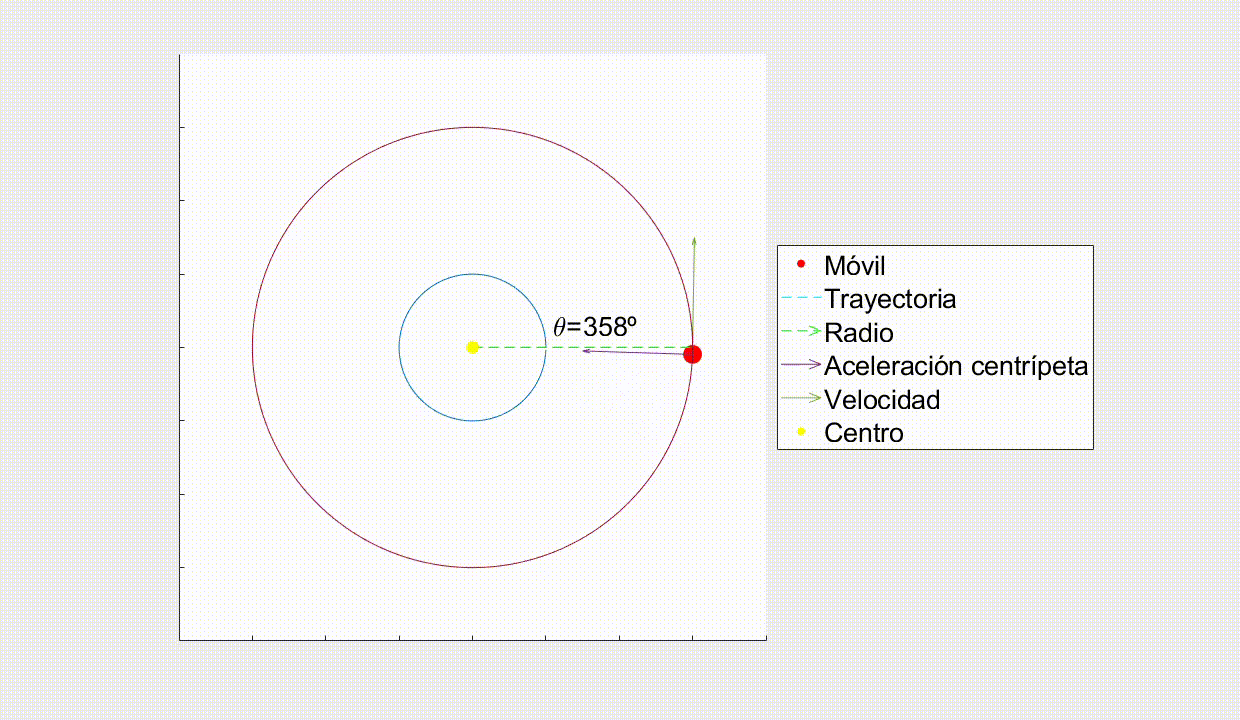Como puedes ver, el vector Aceleración Centrípeta y el vector Radio son paralelos, lo que hace que el Momento Angular se conserve.