Tabla de contenidos
Leyes De Newton
Las Leyes de Newton reciben su nombre de Isaac Newton, quien las mostró por primera vez con la publicación en 1687 de su libro Principia. En ellas se basa la Mecánica Clásica, es decir, toda la Dinámica anterior al siglo XX está fundamentada en estas 3 leyes:
- 1ª Ley de Newton o Principio de Inercia: "Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él " ^{1}. Es decir, si un cuerpo está parado o describe un MRU, seguirá así si ninguna fuerza actúa sobre él.
\sum \vec{F}=0 \rightarrow \vec{v}=cte.
- 2ª Ley de Newton o Ley Fundamental de la Dinámica: "El cambio de movimiento es directamente proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime " ^{2}«. Es decir, el cambio de movimiento, lo que es lo mismo, el cambio de momento lineal \vec{p} es un vector cuyo módulo es directamente proporcional a la Fuerza que se aplica en el cuerpo, y tiene como dirección y sentido el de la Fuerza aplicada \vec{F}:
\vec{F} \, = \, \frac{d\vec{p}}{dt} \, = \, \frac{dm}{dt}\vec{v}+m \vec{a}
|\vec{F}|=kg \, m/s^{2} \, = \, N
De esta fórmula podemos extraer un casos específico: la masa m es constante, por lo que \frac{dm}{dt} \, = \, 0, por lo que:
\vec{F}=m\vec{a}
Que es la formulación más conocida de la Segunda Ley y una de las fórmulas más conocidas e importantes de la Física.
- 3ª Ley de Newton o Principio de Equivalencia: "Con toda acción ocurre siempre una reacción igual y contraria: quiere decir que las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto" ^{3}. Es decir, si aplicas una fuerza sobre un cuerpo, el cuerpo responderá aplicando la misma fuerza sobre ti, es lo que ocurre, por ejemplo, cuando remas en una barca:
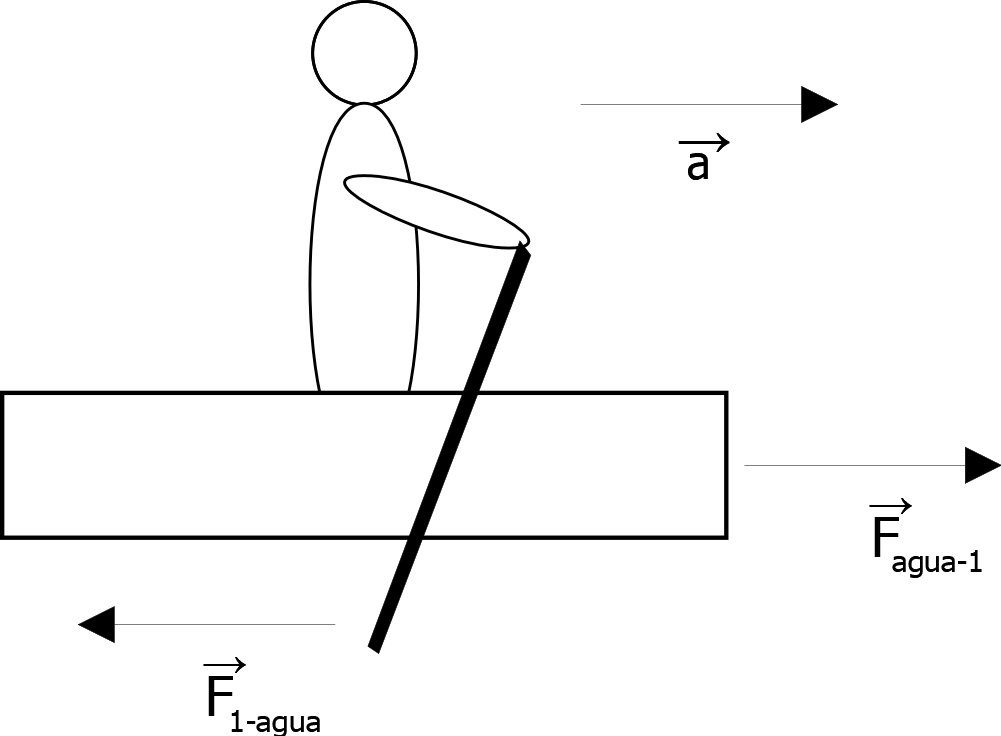
\vec{F}_{1-agua} \, = \, -\vec{F}_{agua-1}
F_{1-agua} \, = \, F_{agua-1}
Principio de Superposición:
El Principio de Superposición nos indica que si actúan varias Fuerzas sobre un cuerpo, la Fuerza total neta sobre el cuerpo es igual a la suma (vectorial) de todas las fuerzas individuales:
\vec{F}_{Total}\, = \, \vec{F}_{1}+\vec{F}_{2}+\vec{F}_{3}+…
Interactúa con el gráfico, mueve los puntos para cambiar las Fuerzas y ver la resultante.
Relación del Momento Lineal con las Fuerzas.
A través del Momento Lineal y su conservación, podemos derivar todas las Leyes de Newton:
- Primera Ley de Newton: es consecuencia directa de la conservación del Momento Lineal, si no hay ninguna fuerza actúa sobre un cuerpo, conservará su Momento por lo que mantendrá un MRU.
- Segunda Ley de Newton: que define Fuerza como el cambio temporal del momento lineal (\vec{F} \, = \, \frac{d\vec{p}}{dt})
- Tercera Ley de Newton: también consecuencia del Momento Lineal. De la Segunda Ley hemos sacado que la Fuerza es un intercambio de Momento, es decir, que un cuerpo le «da» momento a otro, por lo que el que cede debe perder, siendo así que el cambio total de Momento Lineal 0. Que un cuerpo de momento y otro reciba es equivalente a que ambos cuerpos realicen entre sí una fuerza igual y opuesta.
Impulso:
La 2ª Ley permite definir una nueva magnitud vectorial, el Impulso, que se define como la variación de momento debido a una fuerza en un tiempo determinado:
\vec{I}=\Delta \vec{p}=\vec{F}\cdot \Delta t
|I| \, = \, kg \, m/s
- ^{1}Rada García, Eloy (trad.) (2003). «Principios matemáticos de la filosofía natural». apud. Newton. Vida, pensamiento y obra, p. 199. A hombros de gigantes. Las grandes obras de la física y la Astronomía (Barcelona: Crítica).
- ^{2} \, ^{3} Isaac Newton, extractos de Principios matemáticos de la filosofía natural, cit., p. 199.
