Principales Fuerzas

Tras definir las Fuerzas y cómo se comportan mediante las Leyes de Newton, veremos una lista de las principales fuerzas que nos vamos a encontrar en la mayoría de escenarios de la Dinámica:

Fuerza Gravitatoria:

Enunciada por Isaac Newton en su libro Principia, es una fuerza de atracción entre dos cuerpos con masa. Es una Fuerza Conservativa:

\vec{F}_{G}=-\frac{GMm}{r^{2}} \hat r

Donde G es la Constante de Gravitación Universal (G≈6.67 \cdot 10^{-11} \ N \, m^{2}/kg^{2}), M y m las masas de los cuerpos involucrados y \vec{r} el vector que los une. Su potencial asociado es:

E_{G} \, = \, -\frac{GMm}{r}

Peso: 

Es la fuerza a la que está sometido un cuerpo por encontrarse cerca de la superficie de la Tierra. Es perpendicular al suelo y apunta hacia éste. Es una Fuerza Conservativa:

P=m g

Donde g es la aceleración de un cuerpo a nivel del mar (g \, ≈ \, 9.80 \, m/s^{2} ). El potencial asociado al Peso es:

E_{P} \, = \, mgh

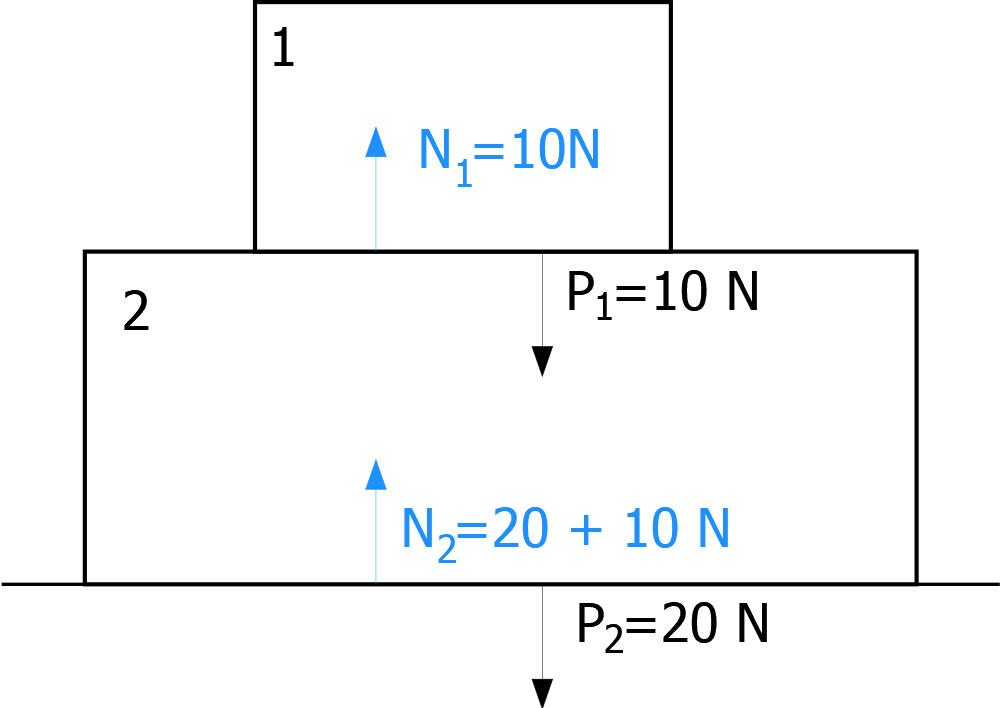
Donde h es la altura sobre el suelo del cuerpo.

Fuerza Normal:

Es la fuerza que hay entre dos cuerpos que están en contacto entre sí. Es la fuerza de repulsión entre los electrones de ambos cuerpos. Es la necesaria y suficiente para que un cuerpo no penetre en el otro. No realiza trabajo.

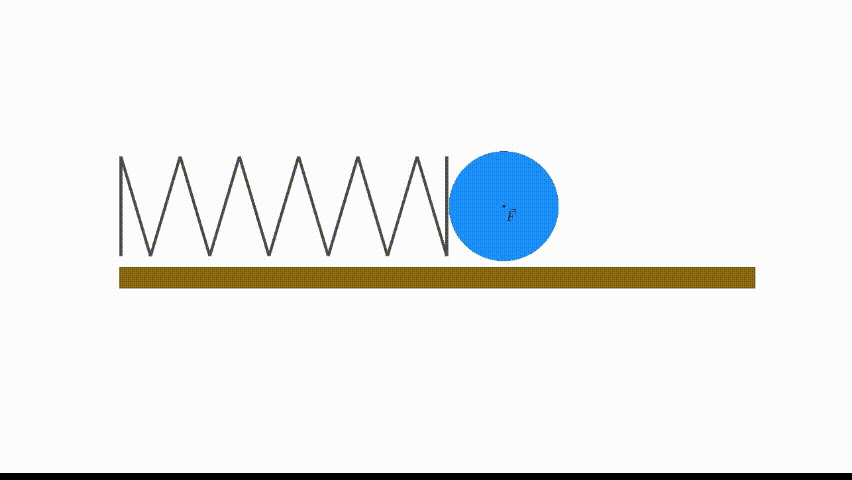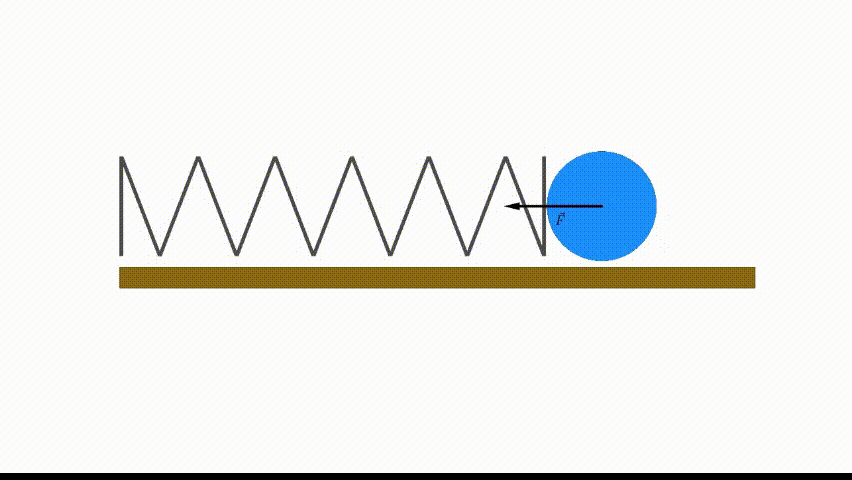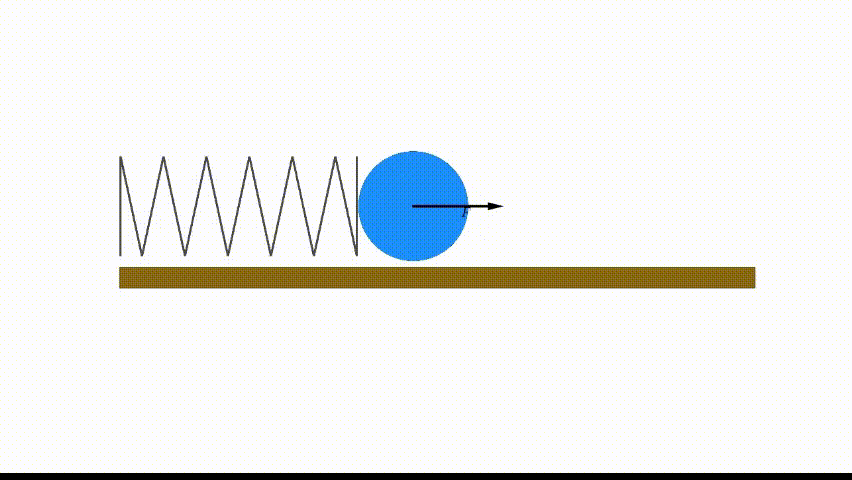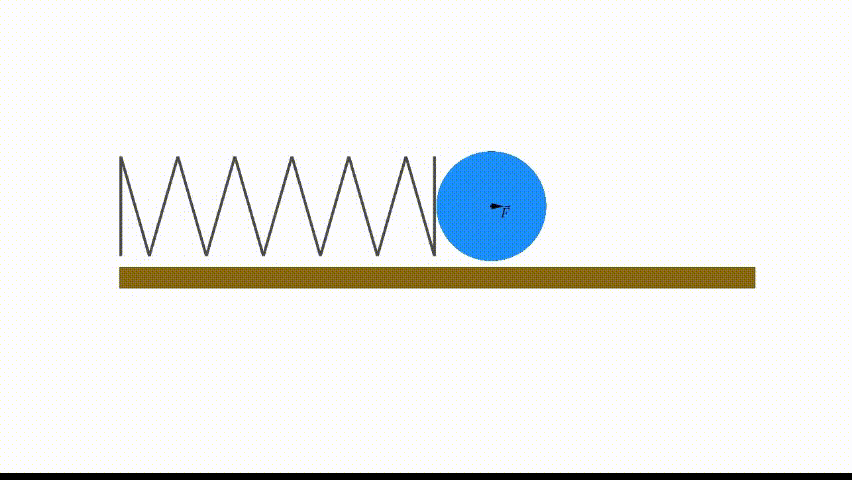
Fuerza Elástica:

Es la fuerza de recuperación que tienen objetos elásticos como cuerdas o muelles. Es una Fuerza Conservativa se explica mediante la Ley de Hooke:

\vec{F}_{e}=-k\vec{r}

Donde k es la constante elástica propia del muelle (|k|=kg/s^{2}) y \vec{r} el vector de desplazamiento del muelle respecto a la posición de equilibrio (donde la elongación es 0, por lo que \vec{F}(eq)=0). El potencial asociado a esta fuerza es:

E_{k} \, = \, \frac{1}{2}k r^{2}

Los cuerpos sometidos a esta fuerza describirán un MAS, donde k \, = \, m \, \omega^{2} y A \, = \, x_{o}, con x_{o} siendo la posición desde donde se suelta al móvil.

Fuerza Eléctrica: 

Aparecen entre cuerpos con carga eléctrica (positiva o negativa). Las cargas de igual signo se repelen y de diferente signo se atraen. Es una Fuerza Conservativa.Se describe mediante la Ley de Coulomb:

F_{E}=\frac{KQq}{r^{2}}

Donde K es la Constante de Coulomb K≈9\cdot 10^{9} \ N \, m^{2}/C^{2}, Q y q el valor absoluto de las cargas involucradas (|Q| \, = \, |q| \, = \, C) y r la distancia entre las cargas. Cuyo potencial asociado es:

E_{E} \, = \,  \frac{KQq}{r}

El signo depende del signo de las cargas.

Fuerza Centrípeta: 

Es la Fuerza Central necesaria para que un cuerpo se mantenga en una trayectoria circular (MCU):

\vec{F}_{c} \, = \, m \, \vec{a}_{c} \, = \, -m \, \frac{v^{2}}{r} \ \hat{r}\, = \, -m \, \omega ^{2} \, \vec{r} 

Es perpendicular en todos los puntos a la trayectoria. No cambia el módulo de la velocidad, sólo su dirección y sentido.

Fuerza de Rozamiento:

Es una Fuerza No Conservativa. Es la Fuerza que se opone al movimiento debido a la repulsión eléctrica entre los electrones en las irregularidades entre dos superficies. Se calcula mediante la fórmula:

F_{roz} \, = \, \mu N

Donde \mu es el coeficiente de rozamiento, y es único para cada par de superficies en contacto y N es el módulo de la Fuerza Normal. La dirección es la de movimiento y el sentido el opuesto al movimiento. Al no ser una Fuerza Conservativa, el Trabajo que realiza no es 0 y se calcula como:

W \, = \, \int \vec{F}_{roz} \cdot d\vec{r}

Como \vec{F}_{roz} no depende de \vec{r}:

W \, = \, F (r_{B} \, – \,  r_{A})