Física Cinemática Movimiento Rectilíneo Uniforme (MRU)
Tabla de contenidos
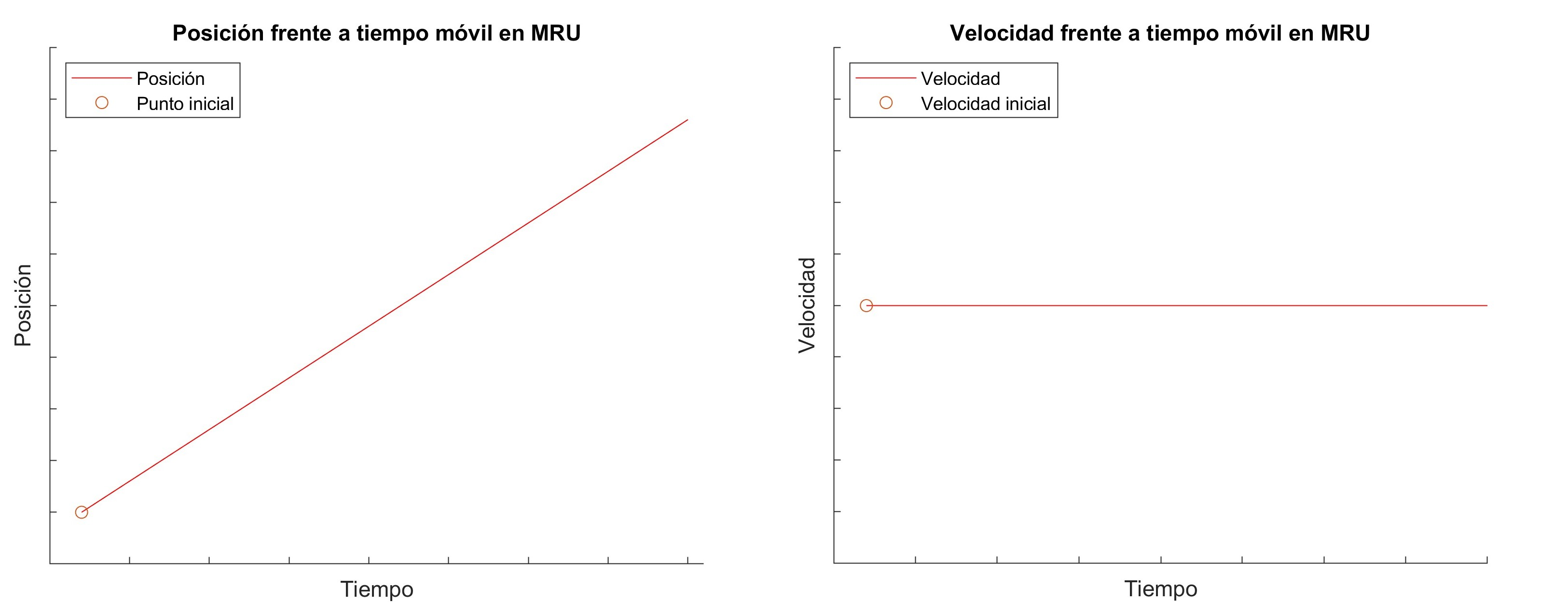
Movimiento Rectilíneo Uniforme (MRU)
Es el caso de los cuerpos que se mueven en línea recta y a velocidad constante, es decir, sin acelerar.
La velocidad instantánea, al ser constante, es igual a la velocidad media y puede calcularse como:
v=\frac{x_{2}-x_{1}}{t_{2}-t_{1}}, [v]=m/s
En el SI, se mide en metros por segundo (m/s).
A partir de esta fórmula, puede deducirse la ecuación de movimiento del MRU, la cual nos permite conocer la posición en función del tiempo x(t) se calcula como:
x(t)=x_{o}+v(t-t_{o}), [x]=m, [t]=s
v=\frac{\varDelta x}{\varDelta t}=\frac{x_{2}-x_{1}}{t_{2}-t_{1}}
Además, el área bajo la recta de la velocidad nos permite calcular la distancia recorrida entre dos puntos de tiempo.
Donde x_{2}, x_{1}, t_{2} y t_{1} son puntos cualesquiera de la recta.
Al ser un movimiento rectilíneo, la velocidad siempre será tangente y paralela al movimiento.
Este movimiento lo describen los cuerpos sobre los que no se aplica ninguna fuerza (o la total es 0), es decir, siguen la Primera Ley de Newton
Derivación de las fórmulas:
Sabiendo que la aceleración es 0, y que a \, = \, \frac{dv}{dt} \, = \, 0, entonces v es constante en el tiempo.
Como v \, = \, \frac{dx}{dt} y v \, = \, cte, entonces v \, = \, \frac{\Delta x}{\Delta t}, de donde sacamos la primera fórmula. Mientras que la segunda es simplemente despejar la x de la primera.
