Física Cinemática Movimiento Circular Uniforme (MCU)
Tabla de contenidos
Movimiento Circular Uniforme (MCU)
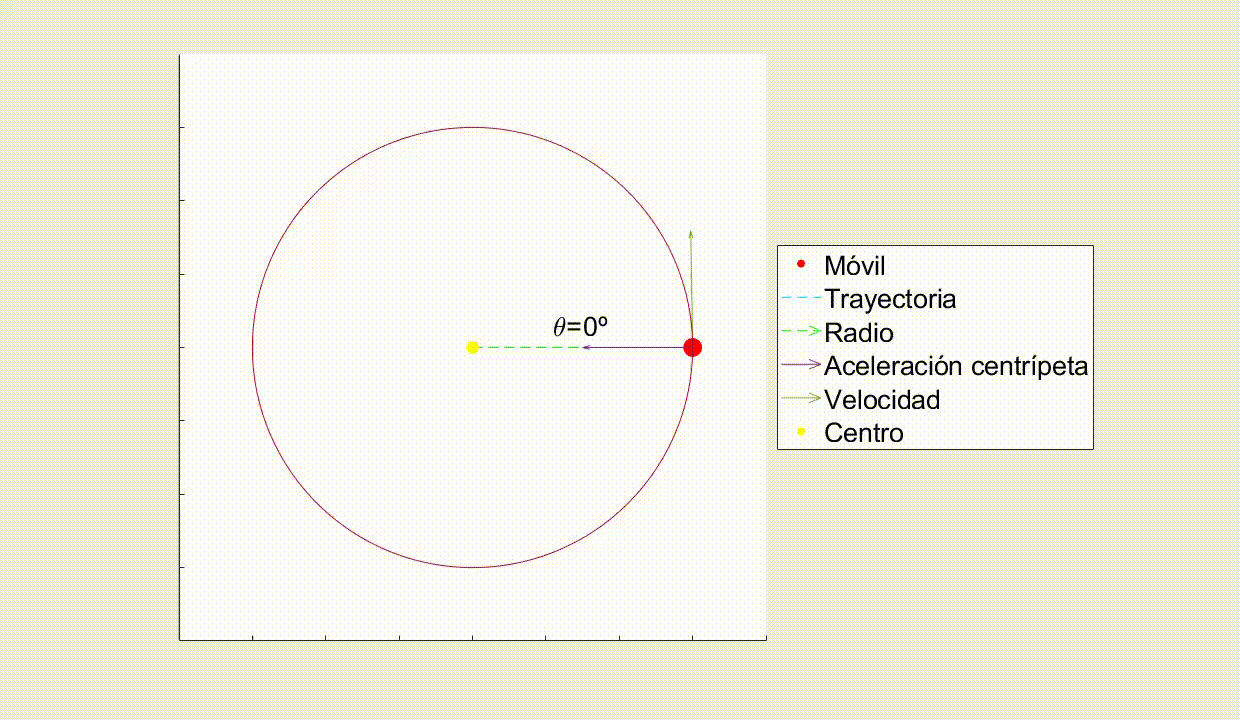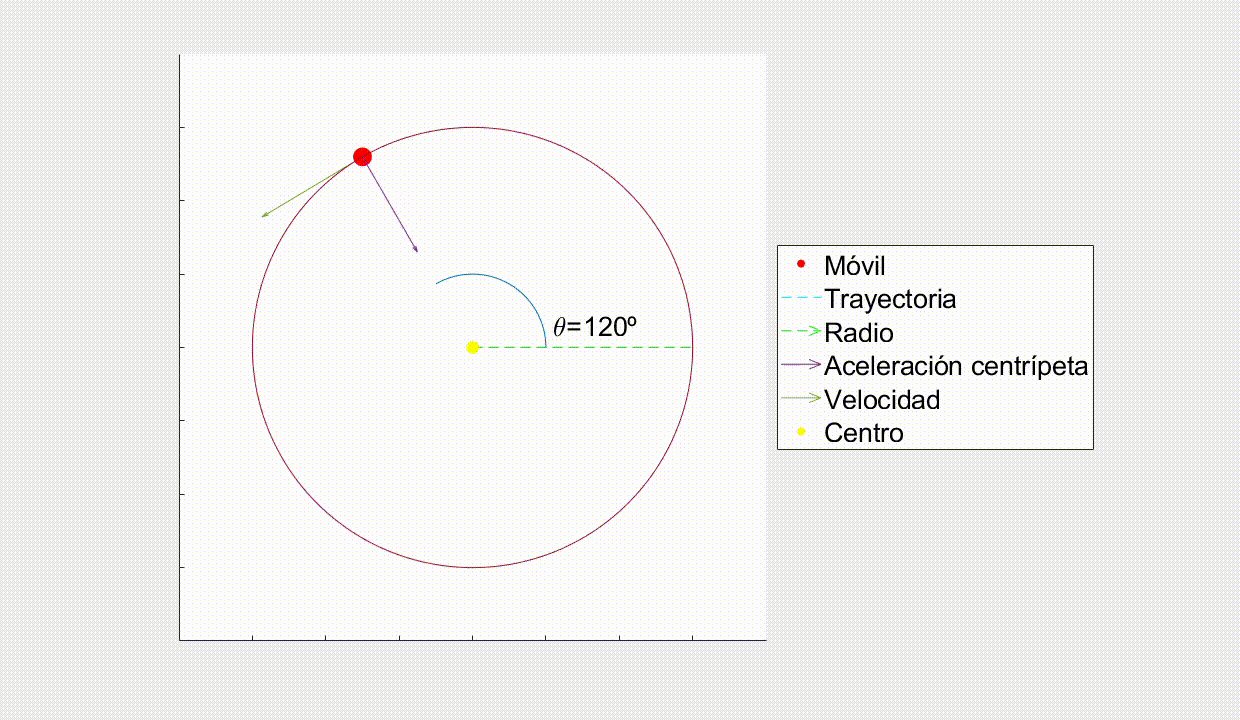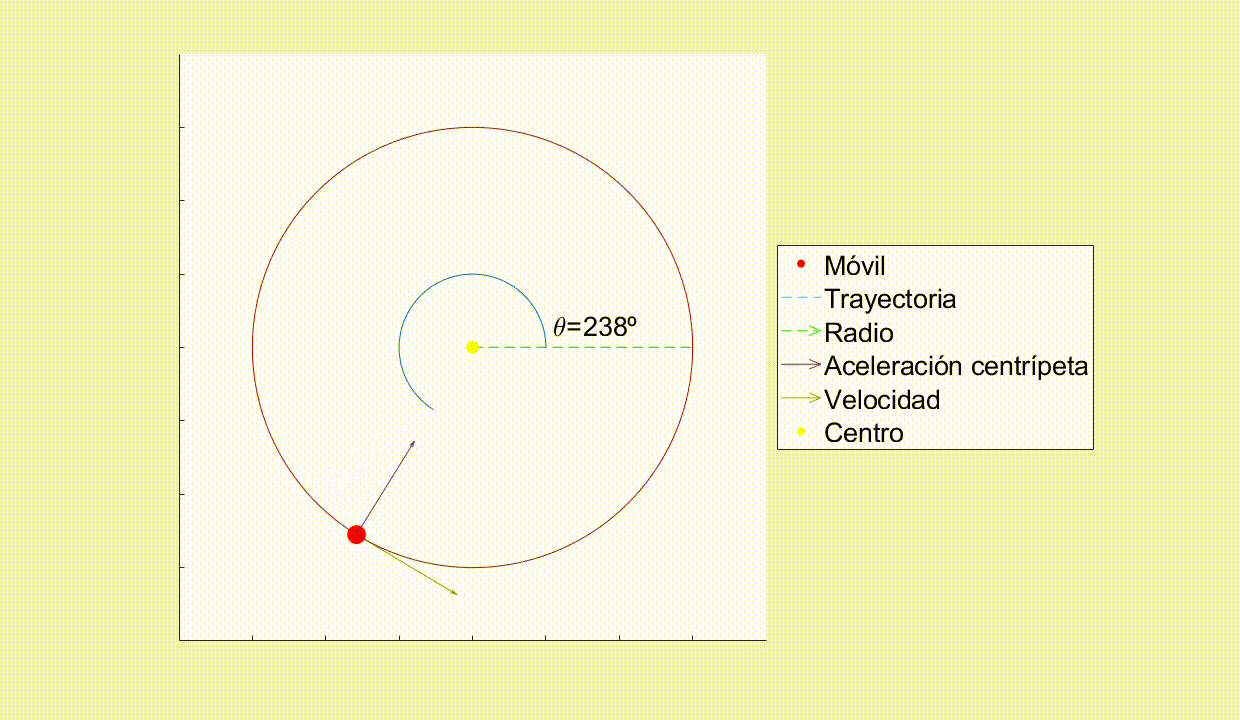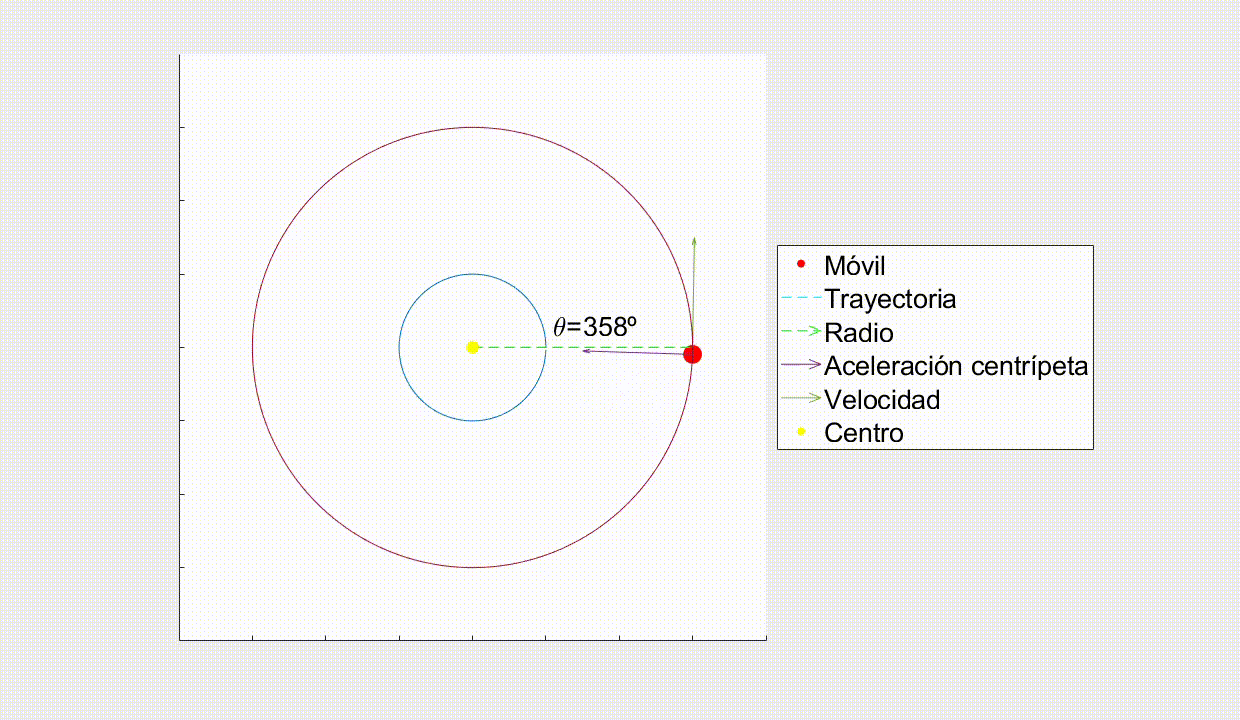
En este movimiento el cuerpo se desplaza en una trayectoria circular cuyo módulo de velocidad es constante, es decir, se encuentra siempre a la misma distancia de un punto central (el radio r)y la velocidad solo cambia en dirección y sentido, no en módulo. Es el que describen, por ejemplo, las ruedas del coche o una noria al girar.
El movimiento circular es periódico, es decir, se repite en el tiempo con una frecuencia determinada. El periodo (T) es el tiempo que tarda en dar una vuelta y la frecuencia (f) es el número de vueltas que da en un tiempo determinado. Se relacionan como: T = 1/f el periodo se mide en segundos (s) y la frecuencia en hercios (Hz=s^{-1}).
En coordenadas polares, podemos determinar la posición mediante el ángulo respecto el eje de referencia \theta (normalmente la horizontal se toma como el 0) y la longitud del radio r. En el SI, los ángulos se miden en radianes, que van desde 0 hasta 2\pi. Para pasar de grados a radianes, hay que usar el factor de conversión 2\pi \, = \, 360º, por ejemplo, 30º \, = \, \frac{\pi}{6} \, rad .
Usando esto, podemos definir la velocidad angular \omega, que es el ángulo que recorre el móvil en un tiempo determinado, se calcula como \omega=\frac{\theta-\theta_{o}}{t-t_{o}} y se mide en el SI en radianes por segundo (rad/s). Sabiendo que en un periodo T el cuerpo completa una vuelta:
\omega=\frac{2\pi}{T}=2\pi f
La velocidad angular es análoga a la velocidad lineal pero para un movimiento giratorio y se relacionan mediante el radio de giro:
v=\omega r
La velocidad es tangencial a la trayectoria en cada punto del movimiento.
Además, podemos calcular la distancia recorrida s como:
s(t)=(\theta – \theta_{o}) \, r \, = \, \omega r \, (t-t_{o}) \, = \, v \, (t-t_{o})
Como el cuerpo está constantemente cambiando de dirección, pero siempre a la misma distancia del centro, necesita una aceleración que no varíe el módulo de la velocidad pero sí su dirección y sentido, ésta es la llamada aceleración centrípeta (a_{c}). Es siempre perpendicular a la trayectoria y con dirección hacia el eje del movimiento. Puede calcularse como:
a_{c}=\omega ^{2}r = \frac{v^{2}}{r}
Además, podemos conocer la posición angular del móvil en función del tiempo \theta (t):
\theta (t) \, = \, \theta_{o} \, + \, \omega \, (t-t_{o}), \ \ [\theta] \, = \, rad
Movimiento Circular Uniformemente Acelerado (MCUA)
En algunos casos, la velocidad angular \omega no es constante, sino que ésta cambia con el tiempo. A la tasa de este cambio se la llama aceleración angular \alpha. Entonces ya no se trata de MCU, sino de Movimiento Circular Uniformemente Acelerado (MCUA). Este movimiento es el que describe, por ejemplo, la ropa dentro de una lavadora que está acelerando/frenando, que cada vez gira más rápido/lento manteniendo el radio de giro.
La descripción del movimiento es prácticamente igual al MCU, sólo que hay que cambiar algunas cosas:
En primer lugar, como \omega no es constante en el tiempo, debemos encontrar una forma de hallar la velocidad angular instantánea, la cual se calcula de la siguiente manera:
\omega (t) \, = \, \omega_{o} \, + \, \alpha(t-t_{o})
Y como cambia \omega, cambia el resto de parámetros del movimiento (menos el radio r):
\theta(t) \, = \, \theta_{o} \, + \, \omega_{o}(t-t_{o}) \, + \, \frac{1}{2}\alpha (t-t_{o})^{2}
T(t) \, = \, \frac{1}{f(t)} \, = \, \frac{2\pi}{\omega_{o}+\alpha(t-t_{o})}
a_{T} \, = \, \alpha r
v(t) \, = \, v_{o} \, + \, a_{T}(t-t_{o})
s(t) \, = \, v_{o}(t-t_{o}) \, + \, a_{T}(t-t_{o})^{2}
Derivación de Fórmulas:
En este caso, las fórmulas de la forma \theta(t) se obtienen de la misma manera que en MRU y MRUA, pero para, en este caso, Coordenadas Polares. Para el caso de las fórmulas del tipo s(t) derivan de saber que s \, = \, r(\theta \, – \, \theta_{o}), es decir, que hay que multiplicar \theta(t) con r
