Tabla de contenidos
Movimiento Armónico Simple (MAS)
El Movimiento Armónico Simple es un movimiento periódico, es decir, que se repite en el tiempo. Los cuerpos que lo describen realizan movimientos de vaivén, como por ejemplo, el de un péndulo.
Este movimiento se caracteriza porque el móvil oscila entre dos puntos de amplitud máxima A a igual distancia de un llamado punto de equilibrio P_{eq}, donde la amplitud considera 0. Al igual que en el MCU, al ser periódico, podemos asociarle al movimiento un periodo T, una frecuencia f y una velocidad angular \omega que se relacionan de igual manera que en el MCU, es decir:
\omega=\frac{2\pi}{T}=2\pi f
Si tomamos, por ejemplo, un péndulo oscilando (ver abajo) y representamos su posición en función del tiempo, obtenemos la gráfica:
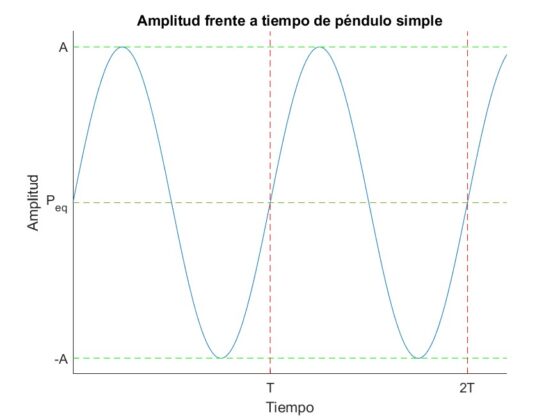
En estas gráficas podemos observar que en los puntos de amplitud máxima, v es 0, mientras que en P_{eq} la velocidad es máxima. Además, de la segunda gráfica podemos ver que la representación de la amplitud en función del tiempo puede describirse mediante una función armónica (seno o coseno), lo que nos da la ecuación de movimiento:
y(t)=A sin(\omega t+\phi_{o})
Donde y(t) representa la amplitud en función del tiempo y \phi_{o}el desfase inicial, que representa el punto del que parte el movimiento (0 para P_{eq}, \frac{\pi}{2} si empieza en A y \frac{-\pi}{2} \ / \ \pi para -A)
Para calcular la ecuación de la velocidad simplemente es derivar y(t) respecto al tiempo, que resulta:
v(t)=\frac{dy}{dt}=\omega Acos(\omega t+\phi_{o})
Cuyo valor absoluto máximo cuando el coseno vale 1 o -1, lo cual corresponde para una posición y(t)=0, donde toma los valores de \omega A y -\omega A para cada momento. Y es 0 cuando el coseno vale 0, que corresponde a los puntos de elongación máxima (A y -A).
Si derivamos la velocidad respecto al tiempo, obtenemos la aceleración del cuerpo en función del tiempo:
a(t)=\frac{dv}{dt}=-\omega ^{2}Asin(\omega t+\phi_{o})
Que es 0 en P_{eq} y máxima (en valor absoluto) en A y -A, donde vale -\omega^{2}A y \omega^{2}A respectivamente.
Derivación de Fórmulas:
Un cuerpo que describe un MAS necesita estar sometido a una fuerza recuperadora (que lleve al cuerpo al punto de equilibrio), esta Fuerza suele ser una Fuerza Elástica de la forma F \, = \, -kx que, usando la Segunda Ley de Newton. Resulta en:
F \, = \, -kx \, = \, ma \, = \, m \frac{d^{2}x}{dt^{2}}
\rightarrow \frac{d^{2}x}{dt^{2}} \, + \, \frac{k}{m}x \, = \, 0
Que es una ecuación diferencial de segundo orden, cuya aproximación para ángulos pequeños es: