Es la suma de Energía Cinética y Energía Potencial.

E_{M} \, = \, E_{c} \, + \, E_{p}

Si únicamente hay Fuerzas Conservativas actuando sobre un cuerpo, la Energía Mecánica se conserva, es decir:

E_{M,o} \, = \, E_{M,f}

E_{c,o} \, + \, E_{p,o} \, = \, E_{c,f} \, + \, E_{p,f}

W \, = \, E_{M,f} \, – \, E_{M,o}

El hecho de que, bajo ciertas condiciones, la Energía Mecánica se conserve es muy útil, y se emplea en una gran cantidad de escenarios en la vida real. Uno en los que mejor se ve esto es en los péndulos:

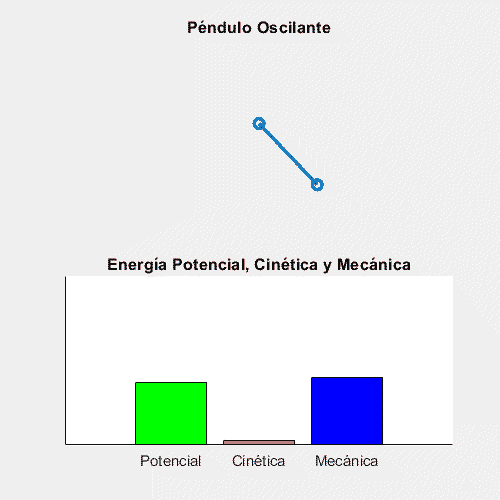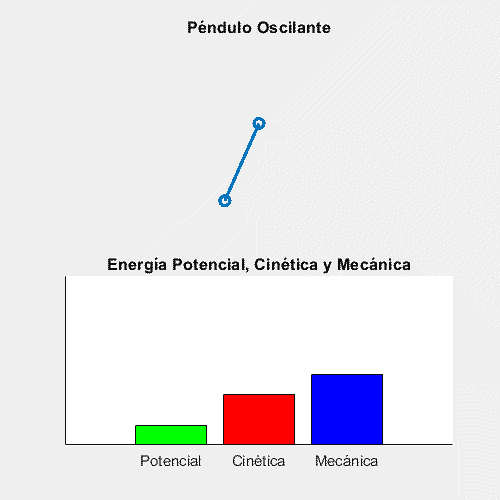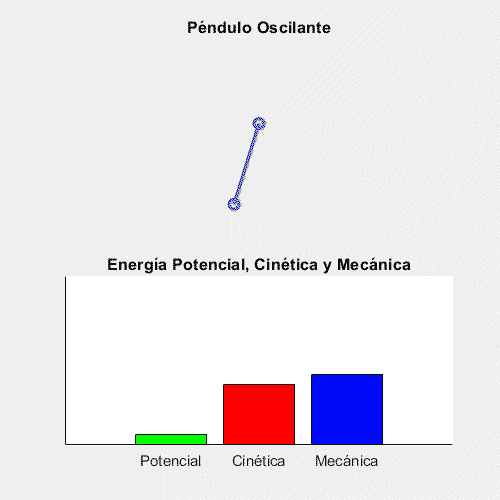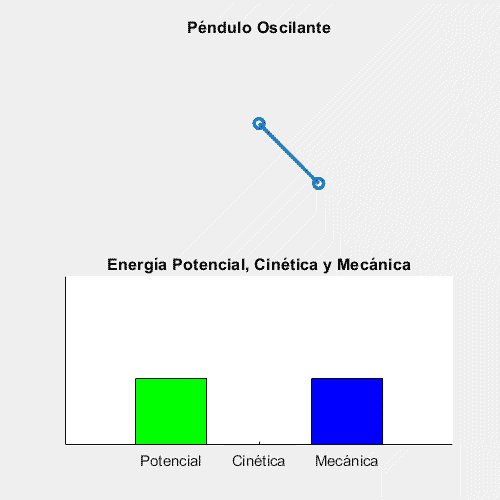
Como se puede ver, en los puntos de amplitud máxima, la Energía Cinética es 0 y la Energía Potencial máxima, mientras que justo cuando pasa por la vertical, la Potencial es 0 y la Cinética es máxima. (Cabe denotar que la energía mecánica no se conserva pues la animación es una aproximación, por lo que se pierde exactitud).

En un péndulo perfecto, el peso oscilará siempre de igual manera entre dos puntos situados simétricamente desde la vertical. Si fuera perfecto y no hubiera rozamiento, esto seguiría así para siempre. Sin embargo, en la vida real pierden Energía con el tiempo y es necesario volver a lanzarlos.